Abstract
Paper is not enough: Crowdsourcing the T1 mapping common ground via the ISMRM reproducibility challenge
*Mathieu Boudreau1,2, *Agah Karakuzu1, Julien Cohen-Adad1,3,4,5, Ecem Bozkurt6, Madeline Carr7,8, Marco Castellaro9, Luis Concha10, Mariya Doneva11, Seraina A. Dual12, Alex Ensworth13,14, Alexandru Foias1, Véronique Fortier15,16, Refaat E. Gabr17, Guillaume Gilbert18, Carri K. Glide-Hurst19, Matthew Grech-Sollars20,21, Siyuan Hu22, Oscar Jalnefjord23,24, Jorge Jovicich25, Kübra Keskin6, Peter Koken11, Anastasia Kolokotronis13,26, Simran Kukran27,28, Nam. G. Lee6, Ives R. Levesque13,29, Bochao Li6, Dan Ma22, Burkhard Mädler30, Nyasha Maforo31,32, Jamie Near33,34, Erick Pasaye10, Alonso Ramirez-Manzanares35, Ben Statton36,Christian Stehning30, Stefano Tambalo25, Ye Tian6, Chenyang Wang37, Kilian Weiss30, Niloufar Zakariaei38, Shuo Zhang30, Ziwei Zhao6, Nikola Stikov1,2,39
- *Authors MB and AK contributed equally to this work
1NeuroPoly Lab, Polytechnique Montréal, Montreal, Quebec, Canada, 2Montreal Heart Institute, Montreal, Quebec, Canada, 3Unité de Neuroimagerie Fonctionnelle (UNF), Centre de recherche de l’Institut Universitaire de Gériatrie de Montréal (CRIUGM), Montreal, Quebec, Canada, 4Mila - Quebec AI Institute, Montreal, QC, Canada, 5Centre de recherche du CHU Sainte-Justine, Université de Montréal, Montreal, QC, Canada, 6Magnetic Resonance Engineering Laboratory (MREL), University of Southern California, Los Angeles, California, USA, 7Medical Physics, Ingham Institute for Applied Medical Research, Liverpool, Australia, 8Department of Medical Physics, Liverpool and Macarthur Cancer Therapy Centres, Liverpool, Australia, 9Department of Information Engineering, University of Padova, Padova, Italy, 10Institute of Neurobiology, Universidad Nacional Autónoma de México Campus Juriquilla, Querétaro, México, 11Philips Research Hamburg, Germany, 12Department of Radiology, Stanford University, Stanford, California, United States, 13Medical Physics Unit, McGill University, Montreal, Canada, 14University of British Columbia, Vancouver, Canada, 15Department of Medical Imaging, McGill University Health Centre, Montreal, Quebec, Canada 16Department of Radiology, McGill University, Montreal, Quebec, Canada, 17Department of Diagnostic and Interventional Imaging, University of Texas Health Science Center at Houston, McGovern Medical School, Houston, Texas, USA, 18MR Clinical Science, Philips Canada, Mississauga, Ontario, Canada, 19Department of Human Oncology, University of Wisconsin-Madison, Madison, Wisconsin, USA, 20Centre for Medical Image Computing, Department of Computer Science, University College London, London, UK, 21Lysholm Department of Neuroradiology, National Hospital for Neurology and Neurosurgery, University College London Hospitals NHS Foundation Trust, London, UK, 22Department of Biomedical Engineering, Case Western Reserve University, Cleveland, Ohio, USA, 23Department of Medical Radiation Sciences, Institute of Clinical Sciences, Sahlgrenska Academy, University of Gothenburg, Gothenburg, Sweden, 24Biomedical Engineering, Sahlgrenska University Hospital, Gothenburg, Sweden, 25Center for Mind/Brain Sciences, University of Trento, Italy, 26Hopital Maisonneuve-Rosemont, Montreal, Canada, 27Bioengineering, Imperial College London, UK, 28Radiotherapy and Imaging, Insitute of Cancer Research, Imperial College London, UK, 29Research Institute of the McGill University Health Centre, Montreal, Canada, 30Clinical Science, Philips Healthcare, Germany, 31Department of Radiological Sciences, University of California Los Angeles, Los Angeles, CA, USA, 32Physics and Biology in Medicine IDP, University of California Los Angeles, Los Angeles, CA, USA, 33Douglas Brain Imaging Centre, Montreal, Canada, 34Sunnybrook Research Institute, Toronto, Canada, 35Computer Science Department, Centro de Investigación en Matemáticas, A.C., Guanajuato, México, 36Medical Research Council, London Institute of Medical Sciences, Imperial College London, London, United Kingdom, 37Department of Radiation Oncology - CNS Service, The University of Texas MD Anderson Cancer Center, Texas, USA, 38Department of Biomedical Engineering, University of British Columbia, British Columbia, Canada, 39Center for Advanced Interdisciplinary Research, Ss. Cyril and Methodius University, Skopje, North Macedonia
Abstract#
Purpose: T1 mapping is a widely used quantitative MRI technique, but its tissue-specific values remain inconsistent across protocols, sites, and vendors. The ISMRM Reproducible Research and Quantitative MR study groups jointly launched a challenge to assess the reproducibility of a well-established inversion recovery T1 mapping technique, with acquisition details published solely as a PDF, on a standardized phantom and in human brains.
Methods: The challenge used the acquisition protocol from Barral et al. 2010. Researchers collected T1 mapping data on the ISMRM/NIST phantom and/or in human brains. Data submission, pipeline development, and analysis were conducted using open-source platforms. Inter-submission and intra-submission comparisons were performed.
Results: Eighteen submissions (39 phantom and 56 human datasets) on scanners by three MRI vendors were collected at 3T (except one, at 0.35T). The mean coefficient of variation (COV) was 6.1% for inter-submission phantom measurements, and 2.9% for intra-submission measurements. For humans, inter-/intra-submission COV was 5.9/3.2% in the genu and 16/6.9% in the cortex. An interactive dashboard for data visualization was also developed: https://rrsg2020.dashboards.neurolibre.org.
Conclusion: The T1 inter-submission variability was twice as high as the intra-submission variability in both phantoms and human brains, indicating that the acquisition details in the selected paper were insufficient to reproduce a quantitative MRI protocol. This study reports the inherent uncertainty in T1 measures across independent research groups, bringing us one step closer to a practical clinical baseline of T1 variations in vivo.
Dashboard: Challenge Submissions
1 | INTRODUCTION#
Significant challenges exist in the reproducibility of quantitative MRI (qMRI) [Keenan et al., 2019]. Despite its promise of improving the specificity and reproducibility of MRI acquisitions, few qMRI techniques have been integrated into clinical practice. Even the most fundamental MR parameters cannot be measured with sufficient reproducibility and precision across clinical scanners to pass the second of six stages of technical assessment for clinical biomarkers [Fryback and Thornbury, 1991, Schweitzer, 2016, Seiberlich et al., 2020]. Half a century has passed since the first quantitative T1 (spin-lattice relaxation time) measurements were first reported as a potential biomarker for tumors [Damadian, 1971], followed shortly thereafter by the first in vivo T1 maps [Pykett and Mansfield, 1978] of tumors, but there is still disagreement in reported values for this fundamental parameter across different sites, vendors, and measurement techniques [Stikov et al., 2015].
Among fundamental MRI parameters, T1 holds significant importance [Boudreau et al., 2020]. T1 represents the time constant for recovery of equilibrium longitudinal magnetization. T1 values will vary depending on the molecular mobility and magnetic field strength [Bottomley et al., 1984, Dieringer et al., 2014, Wansapura et al., 1999]. Knowledge of the T1 values for tissue is crucial for optimizing clinical MRI sequences for contrast and time efficiency [Ernst and Anderson, 1966, Redpath and Smith, 1994, Tofts, 1997] and to calibrate other quantitative MRI techniques [Sled and Pike, 2001, Yuan et al., 2012]. Inversion recovery (IR) [Drain, 1949, Hahn, 1949] is considered the gold standard for T1 measurement due to its robustness against effects like B1 inhomogeneity [Stikov et al., 2015], but its long acquisition times limit the clinical use of IR for T1 mapping [Stikov et al., 2015]. In practice, IR is often used as a reference for validating other T1 mapping techniques, such as variable flip angle imaging (VFA) [Cheng and Wright, 2006, Deoni et al., 2003, Fram et al., 1987], Look-Locker [Look and Locker, 1970, Messroghli et al., 2004, Piechnik et al., 2010], and MP2RAGE [Marques and Gruetter, 2013, Marques et al., 2010].
In ongoing efforts to standardize T1 mapping methods, researchers have been actively developing quantitative MRI phantoms [Keenan et al., 2018]. The International Society for Magnetic Resonance in Medicine (ISMRM) and the National Institute of Standards and Technology (NIST) collaborated on a standard system phantom [Stupic et al., 2021], which was subsequently commercialized (Premium System Phantom, CaliberMRI, Boulder, Colorado). This phantom has since been used in large multicenter studies, such as Bane et al. [Bane et al., 2018] which concluded that acquisition protocols and field strength influence accuracy, repeatability, and interplatform reproducibility. Another NIST-led study [Keenan et al., 2021] found no significant T1 discrepancies among measurements using NIST protocols across 27 MRI systems from three vendors at two clinical field strengths.
The 2020 ISMRM reproducibility challenge 1 posed a slightly different question: can an imaging protocol, independently implemented at multiple centers, consistently measure one of the fundamental MRI parameters (T1)? To assess this, we proposed using inversion recovery on a standardized phantom (ISMRM/NIST system phantom) and the healthy human brain. Specifically, this challenge explored whether the acquisition details provided in a seminal paper on T1 mapping [Barral et al., 2010] is sufficient to ensure the reproducibility across independent research groups.
2 | METHODS#
2.1 | Phantom and human data#
The challenge asked researchers with access to the ISMRM/NIST system phantom [Stupic et al., 2021] (Premium System Phantom, CaliberMRI, Boulder, Colorado) to measure T1 maps of the phantom’s T1 plate (Table 1). Researchers who participated in the challenge were instructed to record the temperature before and after scanning the phantom using the phantom’s internal thermometer. Instructions for positioning and setting up the phantom were devised by NIST and were provided to researchers through the NIST website 2. In brief, the instructions explained how to orient the phantom and how long the phantom should be in the scanner room prior to scanning to achieve thermal equilibrium.
Sphere |
Version 1 (ms) |
Version 2 (ms) |
|---|---|---|
1 |
1989 ± 1.0 |
1883.97 ± 30.32 |
2 |
1454 ± 2.5 |
1330.16 ± 20.41 |
3 |
984.1 ± 0.33 |
987.27 ± 14.22 |
4 |
706 ± 1.0 |
690.08 ± 10.12 |
5 |
496.7 ± 0.41 |
484.97 ± 7.06 |
6 |
351.5 ± 0.91 |
341.58 ± 4.97 |
7 |
247.13 ± 0.086 |
240.86 ± 3.51 |
8 |
175.3 ± 0.11 |
174.95 ± 2.48 |
9 |
125.9 ± 0.33 |
121.08 ± 1.75 |
10 |
89.0 ± 0.17 |
85.75 ± 1.24 |
11 |
62.7 ± 0.13 |
60.21 ± 0.87 |
12 |
44.53 ± 0.090 |
42.89 ± 0.44 |
13 |
30.84 ± 0.016 |
30.40 ± 0.62 |
14 |
21.719 ± 0.005 |
21.44 ± 0.31 |
Researchers were also instructed to collect T1 maps in healthy human brains, and were asked to measure a single slice positioned parallel to the anterior commissure - posterior commissure (AC-PC) line. Prior to imaging, the imaging subjects consented 4 to share their de-identified data with the challenge organizers and on the Open Science Framework (OSF.io) website. As the submitted data was a single slice, the researchers were not instructed to de-face the data of their imaging subjects. Researchers submitting human data provided written confirmation to the organizers that their data was acquired in accordance with their institutional ethics committee (or equivalent regulatory body) and that the subjects had consented to data sharing as outlined in the challenge.
2.2 | MRI Acquisition Protocol#
Researchers followed the inversion recovery T1 mapping protocol optimized for the human brain as described in the paper published by Barral et al. [Barral et al., 2010], which used: TR = 2550 ms, TIs = 50, 400, 1100, 2500 ms, TE = 14 ms, 2 mm slice thickness and 1×1 mm2 in-plane resolution. Note that this protocol is not suitable for fitting models that assume TR > 5T1. Instead, the more general Barral et al. [Barral et al., 2010] fitting model described in Section 2.4 can be used, and this model is compatible with both magnitude-only and complex data. Researchers were instructed to closely adhere to this protocol and report any deviations due to technical limitations.
2.3 | Data Submissions#
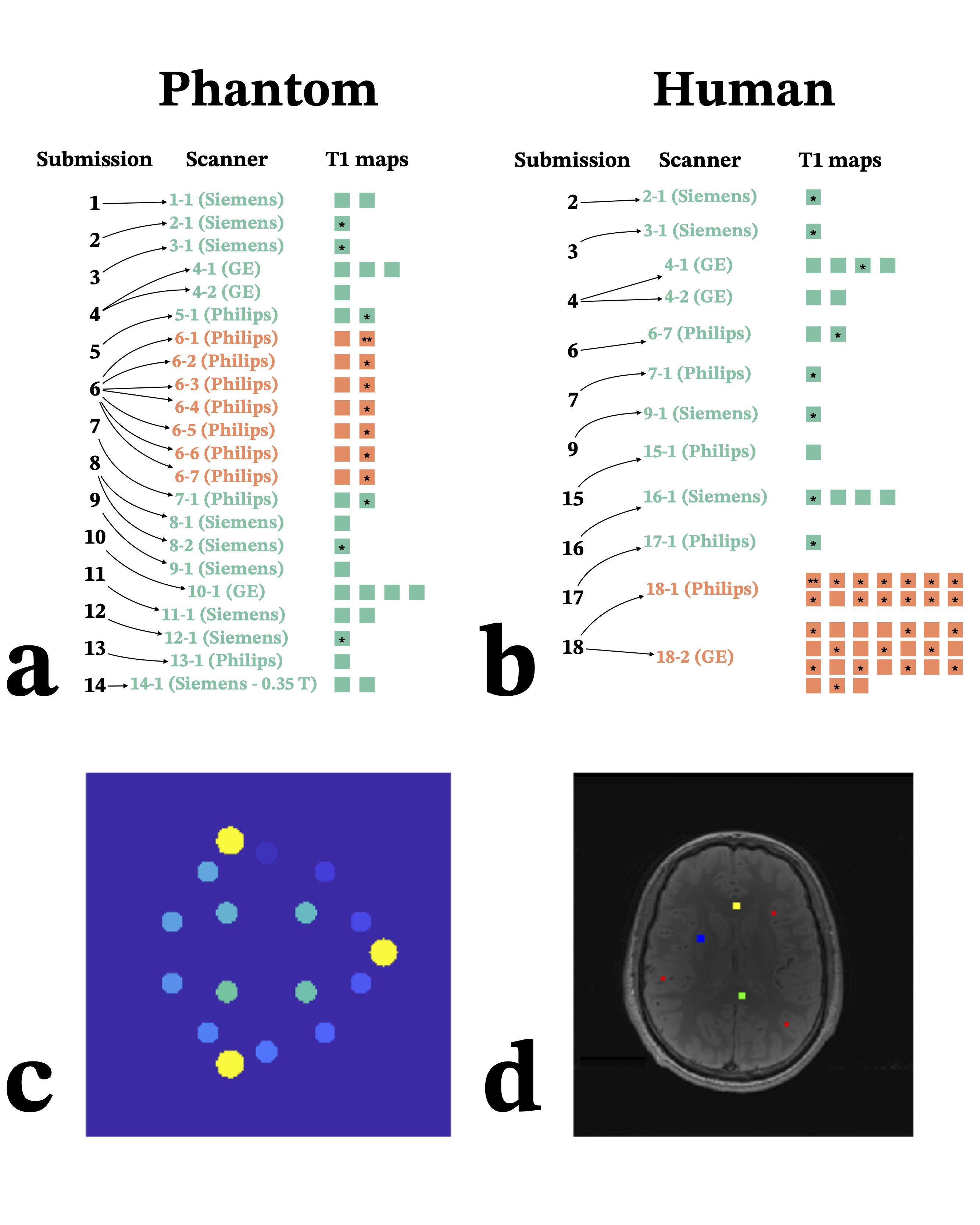
Data submissions for the challenge were handled through a GitHub repository (https://github.com/rrsg2020/data_submission), enabling a standardized and transparent process. All datasets were converted to the NIfTI format, and images for all TIs were concatenated into a single NIfTI file. Each submission included a YAML file to store additional information (submitter details, acquisition details, and phantom or human subject details). Submissions were reviewed 5, and following acceptance the datasets were uploaded to OSF.io (osf.io/ywc9g/). A Jupyter Notebook [Kluyver et al., 2016, Beg et al., 2021] pipeline using qMRLab [Cabana et al., 2015, Karakuzu et al., 2020] was used to process the T1 maps and to conduct quality-control checks. MyBinder links to Jupyter notebooks that reproduced each T1 map were shared in each respective submission GitHub issue to easily reproduce the results in web browsers while maintaining consistent computational environments. Eighteen submissions were included in the analysis, which resulted in 39 T1 maps of the NIST/system phantom, and 56 brain T1 maps. Figure 1 illustrates all the submissions that acquired phantom data (Figure 1-a) and human data (Figure 1-b), the MRI scanner vendors, and the resulting T1 mapping datasets. Some submissions included measurements where both complex and magnitude-only data from the same acquisition were used to fit T1 maps, thus the total number of unique acquisitions is lower than the numbers reported above (27 for phantom data and 44 for human data). The datasets were collected on systems from three MRI manufacturers (Siemens, GE, Philips) and were acquired at 3T 6, except for one dataset acquired at 0.35T (the ViewRay MRidian MR-linac).
Figure 1. List of the datasets submitted to the challenge. Submissions that included phantom data are shown in a), and those that included human brain data are shown in b). For the phantom (panel a), each submission acquired its data using a single phantom, but some researchers shared the same physical phantom with each other. Green indicates submissions used for inter-submission analyses, and orange indicates the sites used for intra-submission analyses. T1 maps used in the calculations of inter- (green) and intra- (orange) submission coefficients of variation (COV) are indicated with asterisks. Images c) and d) illustrate the ROI choice in phantoms and humans.
2.4 | Fitting Model and Pipeline#
A reduced-dimension non-linear least squares (RD-NLS) approach was used to fit the complex general inversion recovery signal equation:
where a and b are complex constants. This approach, developed by Barral et al. [Barral et al., 2010], offers a model for the general T1 signal equation without relying on the long-TR approximation. The a and b constants inherently factor TR in them, as well as other imaging parameters such as excitation pulse angle, inversion pulse flip angles, TR, TE, TI, and a constant that has contributions from T2 and the receive coil sensitivity. Barral et al. [31] shared their MATLAB (MathWorks, Natick, MA) code for the fitting algorithm used in their paper 7. Magnitude-only data were fitted to a modified version of Eq. 1 (Eq. 15 of Barral et al. 2010) with signal-polarity restoration by finding the signal minima, fitting the inversion recovery curve for two cases (data points for TI < TIminimum flipped, and data points for TI ≤ TIminimum flipped), and selecting the case that resulted in the best fit based on minimizing the residual between the model and the measurements 8. This code is available as part of the open-source software qMRLab [Cabana et al., 2015, Karakuzu et al., 2020], which provides a standardized application program interface (API) to call the fitting in MATLAB/Octave scripts.
A data processing pipeline was written using MATLAB/Octave in a Jupyter Notebook. This pipeline downloads every dataset from OSF.io (osf.io/ywc9g/), loads its configuration file, fits the T1 maps, and then saves them to NIfTI and PNG formats. The code is available on GitHub (https://github.com/rrsg2020/t1_fitting_pipeline, filename: RRSG_T1_fitting.ipynb). Finally, T1 maps were manually uploaded to OSF (osf.io/ywc9g/).
2.5 | Image Labeling & Registration#
The T1 plate (NiCl2 array) of the phantom has 14 spheres that were labeled as the regions-of-interest (ROI) using a numerical mask template created in MATLAB, provided by NIST researchers (Figure 1-c). To avoid potential edge effects in the T1 maps, the ROI labels were reduced to 60% of the expected sphere diameter. A registration pipeline in Python using the Advanced Normalization Tools (ANTs) [Avants et al., 2009] was developed and shared in the analysis repository of our GitHub organization (https://github.com/rrsg2020/analysis, filename: register_t1maps_nist.py, commit ID: 8d38644). Briefly, a label-based registration was first applied to obtain a coarse alignment, followed by an affine registration (gradientStep: 0.1, metric: cross correlation, number of steps: 3, iterations: 100/100/100, smoothness: 0/0/0, sub-sampling: 4/2/1) and a BSplineSyN registration (gradientStep:0.5, meshSizeAtBaseLevel:3, number of steps: 3, iterations: 50/50/10, smoothness: 0/0/0, sub-sampling: 4/2/1). The ROI labels template was nonlinearly registered to each T1 map uploaded to OSF.
For human data, manual ROIs were segmented by a single researcher (M.B., 11+ years of neuroimaging experience) using FSLeyes [McCarthy, 2019] in four regions (Figure 1-d): located in the genu, splenium, deep gray matter, and cortical gray matter. Automatic segmentation was not used because the data were single-slice and there was inconsistent slice positioning between datasets.
2.6 | Analysis and Statistics#
Analysis code and scripts were developed and shared in a version-controlled public GitHub repository 9. The T1 fitting and data analysis were performed by M.B., one of the challenge organizers. Computational environment requirements were containerized in Docker [Boettiger, 2015, Merkel, 2014] to create an executable environment that allows for analysis reproduction in a web browser via MyBinder 10 [Project Jupyter et al., 2018]. Backend Python files handled reference data, database operations, ROI masking, and general analysis tools. Configuration files handled dataset information, and the datasets were downloaded and pooled using a script (make_pooled_datasets.py). The databases were created using a reproducible Jupyter Notebook script and subsequently saved in the repository.
The mean T1 values of the ISMRM/NIST phantom data for each ROI were compared with temperature-corrected reference values and visualized in three different types of plots (linear axes, log-log axes, and error relative to the reference value). Temperature correction involved nonlinear interpolation 11 of a NIST reference table of T1 values for temperatures ranging from 16 °C to 26 °C (2 °C intervals) as specified in the phantom’s technical specifications. For the human datasets, the mean and standard deviations for each tissue ROI were calculated from all submissions across all sites. Two submissions (one of phantom data – submission 6 in Figure 1-a, and one of human data – submission 18 in Figure 1-b) were received that measured large T1 mapping datasets. Submission 6 consisted of data from one traveling phantom acquired at seven Philips imaging sites, and submission 18 was a large cohort of volunteers that were imaged on two 3T scanners, one GE and one Philips. These datasets (identified in orange in Figures 1, 3, and 4) were used to calculate intra-submission coefficients of variation (COV) (one per scanner/volunteer, identified by asterisks in Figure 1-a and 1-b), and inter-submission COVs were calculated using one T1 map from each of these (orange) along with one from all other submissions 12 (identified as green in Figures 1, 3, and 4, and the T1 maps used in those COV calculations are also indicated with asterisks in Figure 1-a and 1-b). All quality assurance and analysis plot images were stored in the repository. Additionally, the database files of ROI values and acquisition details for all submissions were also stored in the repository.
2.7 | Dashboard#
To widely disseminate the challenge results, a web-based dashboard was developed (Figure 2, https://rrsg2020.dashboards.neurolibre.org). The landing page (Figure 2-a) showcases the relationship between the phantom and brain datasets acquired at different sites/vendors. Selecting the Phantom or In Vivo icons and then clicking a ROI will display whisker plots for that region. Additional sections of the dashboard allow for displaying statistical summaries for both sets of data, a magnitude vs complex data fitting comparison, and hierarchical shift function analyses.
Figure 2 Dashboard. a) Welcome page listing all the sites, the types of subject, and scanner vendor, and the relationship between the three. b) The phantom tab for a selected ROI, and c) The in vivo tab for a selected ROI. Link: [https://rrsg2020.dashboards.neurolibre.org](https://rrsg2020.dashboards.neurolibre.org)
3 | RESULTS#
Figure 3 presents a comprehensive overview of the challenge results through violin plots, depicting inter- and intra- submission comparisons in both phantoms (a) and human (b) datasets. For the phantom (Figure 3-a), the average inter-submission COV for the first five spheres, representing the expected T1 value range in the human brain (approximately 500 to 2000 ms) was 6.1%. By addressing outliers from two sites associated with specific challenges for sphere 4 (signal null near a TI), the mean inter-submission COV was reduced to 4.1%. One participant (submission 6, Figure 1) measured T1 maps using a consistent protocol at 7 different sites, and the mean intra-submission COV across the first five spheres for this submission was calculated to be 2.9%.
For the human datasets (Figure 3-b), inter-submission COVs for independently-implemented imaging protocols were 5.9% for genu, 10.6 % for splenium, 16 % for cortical GM, and 22% for deep GM. One participant (submission 18, Figure 1) measured a large dataset (13 individuals) on three scanners and two vendors, and the intra-submission COVs for this submission were 3.2% for genu, 3.1% for splenium, 6.9% for cortical GM, and 7.1% for deep GM. The binomial appearance for the splenium, deep GM, and cortical GM for the sites used in the inter-site analyses (green) can be explained by an outlier measurement, which can be seen in (Figure 4 e-f, site 3.001).
# Imports
import os
import shutil
from pathlib import Path
from os import path
import pandas as pd
import numpy as np
if build == 'latest':
if path.isdir('analysis')== False:
!git clone https://github.com/rrsg2020/analysis.git
dir_name = 'analysis'
analysis = os.listdir(dir_name)
for item in analysis:
if item.endswith(".ipynb"):
os.remove(os.path.join(dir_name, item))
if item.endswith(".md"):
os.remove(os.path.join(dir_name, item))
elif build == 'archive':
if os.path.isdir(Path('../data')):
data_path = ['../data/rrsg-2020-note/rrsg-2020-neurolibre']
else:
# define data requirement path
data_req_path = os.path.join("..", "binder", "data_requirement.json")
# download data
repo2data = Repo2Data(data_req_path)
data_path = repo2data.install()
from analysis.src.database import *
import matplotlib.pyplot as plt
plt.style.use('analysis/custom_matplotlibrc')
plt.rcParams["figure.figsize"] = (20,5)
fig_id = 0
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)
pd.set_option('display.width', 1000)
pd.set_option('display.colheader_justify', 'center')
pd.set_option('display.precision', 1)
# Configuration
database_path = Path('analysis/databases/3T_NIST_T1maps_database.pkl')
remove_outliers = False
# Load database
df = pd.read_pickle(database_path)
# Prepare stats table
columns = [
'1',
'2',
'3',
'4',
'5',
'6',
'7',
'8',
'9',
'10',
'11',
'12',
'13',
'14'
]
col_vals = [
None,
None,
None,
None,
None,
None,
None,
None,
None,
None,
None,
None,
None,
None
]
df_setup = {
'all submissions mean T1': col_vals,
'inter-submission mean T1': col_vals,
'intra-submission mean T1': col_vals,
'all submissions T1 STD': col_vals,
'inter-submission T1 STD': col_vals,
'intra-submission T1 STD': col_vals,
'all submissions COV [%]': col_vals,
'inter-submission COV [%]': col_vals,
'intra-submission COV [%]': col_vals
}
stats_table = pd.DataFrame.from_dict(df_setup, orient='index', columns=columns)
## Inter-submission stats (phantom version 1)
# One subject/measurement per submission were selected. The protocol closest to the proposed one was selected, preferring complex data over magnitude-only.
# Selecting one subject/measurement per submission, protocol closest to proposed, complex if available.
ids_intersubmissions = (
2.001,
3.001,
5.002,
6.002,
8.001,
12.001,
)
estimate_1 = np.array([])
estimate_2 = np.array([])
estimate_3 = np.array([])
estimate_4 = np.array([])
estimate_5 = np.array([])
estimate_6 = np.array([])
estimate_7 = np.array([])
estimate_8 = np.array([])
estimate_9 = np.array([])
estimate_10 = np.array([])
estimate_11 = np.array([])
estimate_12 = np.array([])
estimate_13 = np.array([])
estimate_14 = np.array([])
print(estimate_1.size)
ii = 0
for index in ids_intersubmissions:
if index == 13.001: # missing data
break
if remove_outliers and (index == 12.001 or index == 2.001):
pass
else:
if df.loc[index]['phantom serial number']<42: # version 1
pass
else:
if df.loc[index]['phantom serial number'] is None:
df.at[index, 'phantom serial number'] = 999 # Missing phantom number was version 2, see discussion here https://github.com/rrsg2020/data_submission/issues/25#issuecomment-620045155
estimate_1 = np.append(estimate_1, np.mean(df.loc[index]['T1 - NIST sphere 1']))
estimate_2 = np.append(estimate_2, np.mean(df.loc[index]['T1 - NIST sphere 2']))
estimate_3 = np.append(estimate_3, np.mean(df.loc[index]['T1 - NIST sphere 3']))
estimate_4 = np.append(estimate_4, np.mean(df.loc[index]['T1 - NIST sphere 4']))
estimate_5 = np.append(estimate_5, np.mean(df.loc[index]['T1 - NIST sphere 5']))
estimate_6 = np.append(estimate_6, np.mean(df.loc[index]['T1 - NIST sphere 6']))
estimate_7 = np.append(estimate_7, np.mean(df.loc[index]['T1 - NIST sphere 7']))
estimate_8 = np.append(estimate_8, np.mean(df.loc[index]['T1 - NIST sphere 8']))
estimate_9 = np.append(estimate_9, np.mean(df.loc[index]['T1 - NIST sphere 9']))
estimate_10 = np.append(estimate_10, np.mean(df.loc[index]['T1 - NIST sphere 10']))
estimate_11 = np.append(estimate_11, np.mean(df.loc[index]['T1 - NIST sphere 11']))
estimate_12 = np.append(estimate_12, np.mean(df.loc[index]['T1 - NIST sphere 12']))
estimate_13 = np.append(estimate_13, np.mean(df.loc[index]['T1 - NIST sphere 13']))
estimate_14 = np.append(estimate_14, np.mean(df.loc[index]['T1 - NIST sphere 14']))
ii = ii +1
stats_table['1']['inter-submission mean T1'] = np.nanmean(estimate_1)
stats_table['1']['inter-submission T1 STD'] = np.nanstd(estimate_1)
stats_table['1']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_1),np.nanmean(estimate_1)) * 100
stats_table['2']['inter-submission mean T1'] = np.nanmean(estimate_2)
stats_table['2']['inter-submission T1 STD'] = np.nanstd(estimate_2)
stats_table['2']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_2),np.nanmean(estimate_2)) * 100
stats_table['3']['inter-submission mean T1'] = np.nanmean(estimate_3)
stats_table['3']['inter-submission T1 STD'] = np.nanstd(estimate_3)
stats_table['3']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_3),np.nanmean(estimate_3)) * 100
stats_table['4']['inter-submission mean T1'] = np.nanmean(estimate_4)
stats_table['4']['inter-submission T1 STD'] = np.nanstd(estimate_4)
stats_table['4']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_4),np.nanmean(estimate_4)) * 100
stats_table['5']['inter-submission mean T1'] = np.nanmean(estimate_5)
stats_table['5']['inter-submission T1 STD'] = np.nanstd(estimate_5)
stats_table['5']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_5),np.nanmean(estimate_5)) * 100
stats_table['6']['inter-submission mean T1'] = np.nanmean(estimate_6)
stats_table['6']['inter-submission T1 STD'] = np.nanstd(estimate_6)
stats_table['6']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_6),np.nanmean(estimate_6)) * 100
stats_table['7']['inter-submission mean T1'] = np.nanmean(estimate_7)
stats_table['7']['inter-submission T1 STD'] = np.nanstd(estimate_7)
stats_table['7']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_7),np.nanmean(estimate_7)) * 100
stats_table['8']['inter-submission mean T1'] = np.nanmean(estimate_8)
stats_table['8']['inter-submission T1 STD'] = np.nanstd(estimate_8)
stats_table['8']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_8),np.nanmean(estimate_8)) * 100
stats_table['9']['inter-submission mean T1'] = np.nanmean(estimate_9)
stats_table['9']['inter-submission T1 STD'] = np.nanstd(estimate_9)
stats_table['9']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_9),np.nanmean(estimate_9)) * 100
stats_table['10']['inter-submission mean T1'] = np.nanmean(estimate_10)
stats_table['10']['inter-submission T1 STD'] = np.nanstd(estimate_10)
stats_table['10']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_10),np.nanmean(estimate_10)) * 100
stats_table['11']['inter-submission mean T1'] = np.nanmean(estimate_11)
stats_table['11']['inter-submission T1 STD'] = np.nanstd(estimate_11)
stats_table['11']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_11),np.nanmean(estimate_11)) * 100
stats_table['12']['inter-submission mean T1'] = np.nanmean(estimate_12)
stats_table['12']['inter-submission T1 STD'] = np.nanstd(estimate_12)
stats_table['12']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_12),np.nanmean(estimate_12)) * 100
stats_table['13']['inter-submission mean T1'] = np.nanmean(estimate_13)
stats_table['13']['inter-submission T1 STD'] = np.nanstd(estimate_13)
stats_table['13']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_13),np.nanmean(estimate_13)) * 100
stats_table['14']['inter-submission mean T1'] = np.nanmean(estimate_14)
stats_table['14']['inter-submission T1 STD'] = np.nanstd(estimate_14)
stats_table['14']['inter-submission COV [%]'] = np.divide(np.nanstd(estimate_14),np.nanmean(estimate_14)) * 100
estimate_1_inter = estimate_1
estimate_2_inter = estimate_2
estimate_3_inter = estimate_3
estimate_4_inter = estimate_4
estimate_5_inter = estimate_5
## Intra-submission stats
# All unique T1 maps from Site 6 were used for the stats calculations. One single vendor, 7 sites. Complex data selected.
# Selecting one submission
ids_intrasubmissions = (
6.002,
6.004,
6.006,
6.008,
6.010,
6.012,
6.014,
)
estimate_1 = np.array([])
estimate_2 = np.array([])
estimate_3 = np.array([])
estimate_4 = np.array([])
estimate_5 = np.array([])
estimate_6 = np.array([])
estimate_7 = np.array([])
estimate_8 = np.array([])
estimate_9 = np.array([])
estimate_10 = np.array([])
estimate_11 = np.array([])
estimate_12 = np.array([])
estimate_13 = np.array([])
estimate_14 = np.array([])
ii = 0
for index in ids_intrasubmissions:
if index == 13.001: # missing data
break
if remove_outliers and (index == 12.001 or index == 2.001):
pass
else:
estimate_1 = np.append(estimate_1, np.mean(df.loc[index]['T1 - NIST sphere 1']))
estimate_2 = np.append(estimate_2, np.mean(df.loc[index]['T1 - NIST sphere 2']))
estimate_3 = np.append(estimate_3, np.mean(df.loc[index]['T1 - NIST sphere 3']))
estimate_4 = np.append(estimate_4, np.mean(df.loc[index]['T1 - NIST sphere 4']))
estimate_5 = np.append(estimate_5, np.mean(df.loc[index]['T1 - NIST sphere 5']))
estimate_6 = np.append(estimate_6, np.mean(df.loc[index]['T1 - NIST sphere 6']))
estimate_7 = np.append(estimate_7, np.mean(df.loc[index]['T1 - NIST sphere 7']))
estimate_8 = np.append(estimate_8, np.mean(df.loc[index]['T1 - NIST sphere 8']))
estimate_9 = np.append(estimate_9, np.mean(df.loc[index]['T1 - NIST sphere 9']))
estimate_10 = np.append(estimate_10, np.mean(df.loc[index]['T1 - NIST sphere 10']))
estimate_11 = np.append(estimate_11, np.mean(df.loc[index]['T1 - NIST sphere 11']))
estimate_12 = np.append(estimate_12, np.mean(df.loc[index]['T1 - NIST sphere 12']))
estimate_13 = np.append(estimate_13, np.mean(df.loc[index]['T1 - NIST sphere 13']))
estimate_14 = np.append(estimate_14, np.mean(df.loc[index]['T1 - NIST sphere 14']))
ii = ii +1
stats_table['1']['intra-submission mean T1'] = np.nanmean(estimate_1)
stats_table['1']['intra-submission T1 STD'] = np.nanstd(estimate_1)
stats_table['1']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_1),np.nanmean(estimate_1)) * 100
stats_table['2']['intra-submission mean T1'] = np.nanmean(estimate_2)
stats_table['2']['intra-submission T1 STD'] = np.nanstd(estimate_2)
stats_table['2']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_2),np.nanmean(estimate_2)) * 100
stats_table['3']['intra-submission mean T1'] = np.nanmean(estimate_3)
stats_table['3']['intra-submission T1 STD'] = np.nanstd(estimate_3)
stats_table['3']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_3),np.nanmean(estimate_3)) * 100
stats_table['4']['intra-submission mean T1'] = np.nanmean(estimate_4)
stats_table['4']['intra-submission T1 STD'] = np.nanstd(estimate_4)
stats_table['4']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_4),np.nanmean(estimate_4)) * 100
stats_table['5']['intra-submission mean T1'] = np.nanmean(estimate_5)
stats_table['5']['intra-submission T1 STD'] = np.nanstd(estimate_5)
stats_table['5']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_5),np.nanmean(estimate_5)) * 100
stats_table['6']['intra-submission mean T1'] = np.nanmean(estimate_6)
stats_table['6']['intra-submission T1 STD'] = np.nanstd(estimate_6)
stats_table['6']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_6),np.nanmean(estimate_6)) * 100
stats_table['7']['intra-submission mean T1'] = np.nanmean(estimate_7)
stats_table['7']['intra-submission T1 STD'] = np.nanstd(estimate_7)
stats_table['7']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_7),np.nanmean(estimate_7)) * 100
stats_table['8']['intra-submission mean T1'] = np.nanmean(estimate_8)
stats_table['8']['intra-submission T1 STD'] = np.nanstd(estimate_8)
stats_table['8']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_8),np.nanmean(estimate_8)) * 100
stats_table['9']['intra-submission mean T1'] = np.nanmean(estimate_9)
stats_table['9']['intra-submission T1 STD'] = np.nanstd(estimate_9)
stats_table['9']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_9),np.nanmean(estimate_9)) * 100
stats_table['10']['intra-submission mean T1'] = np.nanmean(estimate_10)
stats_table['10']['intra-submission T1 STD'] = np.nanstd(estimate_10)
stats_table['10']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_10),np.nanmean(estimate_10)) * 100
stats_table['11']['intra-submission mean T1'] = np.nanmean(estimate_11)
stats_table['11']['intra-submission T1 STD'] = np.nanstd(estimate_11)
stats_table['11']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_11),np.nanmean(estimate_11)) * 100
stats_table['12']['intra-submission mean T1'] = np.nanmean(estimate_12)
stats_table['12']['intra-submission T1 STD'] = np.nanstd(estimate_12)
stats_table['12']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_12),np.nanmean(estimate_12)) * 100
stats_table['13']['intra-submission mean T1'] = np.nanmean(estimate_13)
stats_table['13']['intra-submission T1 STD'] = np.nanstd(estimate_13)
stats_table['13']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_13),np.nanmean(estimate_13)) * 100
stats_table['14']['intra-submission mean T1'] = np.nanmean(estimate_14)
stats_table['14']['intra-submission T1 STD'] = np.nanstd(estimate_14)
stats_table['14']['intra-submission COV [%]'] = np.divide(np.nanstd(estimate_14),np.nanmean(estimate_14)) * 100
estimate_1_intra = estimate_1
estimate_2_intra = estimate_2
estimate_3_intra = estimate_3
estimate_4_intra = estimate_4
estimate_5_intra = estimate_5
## Violin plot
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# Identify common lengths for each group
lengths = [len(estimate_1_inter), len(estimate_1_intra),
len(estimate_2_inter), len(estimate_2_intra),
len(estimate_3_inter), len(estimate_3_intra),
len(estimate_4_inter), len(estimate_4_intra),
len(estimate_5_inter), len(estimate_5_intra)]
# Find the minimum length
min_length = min(lengths)
# Slice arrays to the minimum length
estimate_1_inter = estimate_1_inter[:min_length]
estimate_1_intra = estimate_1_intra[:min_length]
estimate_2_inter = estimate_2_inter[:min_length]
estimate_2_intra = estimate_2_intra[:min_length]
estimate_3_inter = estimate_3_inter[:min_length]
estimate_3_intra = estimate_3_intra[:min_length]
estimate_4_inter = estimate_4_inter[:min_length]
estimate_4_intra = estimate_4_intra[:min_length]
estimate_5_inter = estimate_5_inter[:min_length]
estimate_5_intra = estimate_5_intra[:min_length]
# Combine data into a single DataFrame
df = pd.DataFrame({
'T1 (ms)': np.concatenate([
estimate_1_inter, estimate_1_intra,
estimate_2_inter, estimate_2_intra,
estimate_3_inter, estimate_3_intra,
estimate_4_inter, estimate_4_intra,
estimate_5_inter, estimate_5_intra
]),
'Group': ['Sphere 1'] * min_length * 2 +
['Sphere 2'] * min_length * 2 +
['Sphere 3'] * min_length * 2 +
['Sphere 4'] * min_length * 2 +
['Sphere 5'] * min_length * 2,
'Type': ['Inter'] * min_length + ['Intra'] * min_length +
['Inter'] * min_length + ['Intra'] * min_length +
['Inter'] * min_length + ['Intra'] * min_length +
['Inter'] * min_length + ['Intra'] * min_length +
['Inter'] * min_length + ['Intra'] * min_length,
'': ['Sphere 1'] * min_length * 2 +
['Sphere 2'] * min_length * 2 +
['Sphere 3'] * min_length * 2 +
['Sphere 4'] * min_length * 2 +
['Sphere 5'] * min_length * 2,
})
from IPython.display import display, HTML
from plotly import __version__
from plotly.offline import init_notebook_mode, iplot, plot
config={
'showLink': False,
'displayModeBar': False,
'toImageButtonOptions': {
'format': 'png', # one of png, svg, jpeg, webp
'filename': 'custom_image',
'height': 400,
'width': 800,
'scale': 2 # Multiply title/legend/axis/canvas sizes by this factor
}
}
init_notebook_mode(connected=True)
from plotly.subplots import make_subplots
import plotly.graph_objects as go
import pandas as pd
# Set the color palette
inter_color='rgb(113, 180, 159)'
intra_color='rgb(233, 150, 117)'
fig = go.Figure()
df1 = pd.DataFrame({
'T1 (ms)': np.concatenate([estimate_1_inter, estimate_2_inter, estimate_3_inter, estimate_4_inter, estimate_5_inter]),
'Group': ['<b>Sphere 1</b>'] * len(estimate_1_inter) + ['<b>Sphere 2</b>'] * len(estimate_2_inter) + ['<b>Sphere 3</b>'] * len(estimate_3_inter) + ['<b>Sphere 4</b>'] * len(estimate_4_inter) + ['<b>Sphere 5</b>'] * len(estimate_5_inter),
'Type': ['Inter'] * len(estimate_1_inter) + ['Inter'] * len(estimate_2_inter) + ['Inter'] * len(estimate_3_inter) + ['Inter'] * len(estimate_4_inter) + ['Inter'] * len(estimate_5_inter) ,
'': ['Sphere 1'] * len(estimate_1_inter) + ['Sphere 2'] * len(estimate_2_inter) + ['Sphere 3'] * len(estimate_3_inter) + ['Sphere 4'] * len(estimate_4_inter) + ['Sphere 5'] * len(estimate_5_inter),
})
df2 = pd.DataFrame({
'T1 (ms)': np.concatenate([estimate_1_intra, estimate_2_intra, estimate_3_intra, estimate_4_intra, estimate_5_intra]),
'Group': ['<b>Sphere 1</b>'] * len(estimate_1_intra) + ['<b>Sphere 2</b>'] * len(estimate_2_intra) + ['<b>Sphere 3</b>'] * len(estimate_3_intra) + ['<b>Sphere 4</b>'] * len(estimate_4_intra) + ['<b>Sphere 5</b>'] * len(estimate_5_intra),
'Type': ['Inter'] * len(estimate_1_intra) + ['Inter'] * len(estimate_2_intra) + ['Inter'] * len(estimate_3_intra) + ['Inter'] * len(estimate_4_intra) + ['Inter'] * len(estimate_5_intra) ,
'': ['Sphere 1'] * len(estimate_1_intra) + ['Sphere 2'] * len(estimate_2_intra) + ['Sphere 3'] * len(estimate_3_intra) + ['Sphere 4'] * len(estimate_4_intra) + ['Sphere 5'] * len(estimate_5_intra),
})
fig.add_trace(go.Violin(x=df1['Group'],
y=df1['T1 (ms)'],
side='negative',
line_color='black',
fillcolor=inter_color,
line=dict(width=1.5),
points=False,
width=1.15,
showlegend=False)
)
fig.add_trace(go.Violin(x=df2['Group'],
y=df2['T1 (ms)'],
side='positive',
line_color='black',
fillcolor=intra_color,
line=dict(width=1.5),
points=False,
width=1.15,
showlegend=False)
)
fig.update_layout(violingap=0, violinmode='overlay')
#fig.show()
fig.update_xaxes(
type="category",
autorange=False,
range=[-0.3,4.7],
dtick=1,
showgrid=False,
gridwidth =1,
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=22,
),
)
fig.update_yaxes(
title='<b>T<sub>1</sub> (ms)</b>',
autorange=False,
range=[300, 2300],
showgrid=True,
dtick=250,
gridcolor='rgb(169,169,169)',
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=22,
),
)
fig.update_layout(
width=800,
height=400,
margin=go.layout.Margin(
l=80,
r=40,
b=80,
t=10,
),
font=dict(
family='Times New Roman',
size=22
),
paper_bgcolor='rgb(255, 255, 255)',
plot_bgcolor='rgb(255, 255, 255)',
annotations=[
dict(
x=-0.1,
y=-0.22,
showarrow=False,
text='<b>a</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=1,
y=0.96,
showarrow=False,
text='<b>Inter-sites</b>',
font=dict(
family='Times New Roman',
size=24,
),
xref='paper',
yref='paper',
bgcolor='rgba(102, 194, 165, 0.8)'
),
dict(
x=1,
y=0.85,
showarrow=False,
text='<b>Intra-sites</b>',
font=dict(
family='Times New Roman',
size=24,
),
xref='paper',
yref='paper',
bgcolor='rgba(252, 141, 98, 0.8)'
),
]
)
# update characteristics shared by all traces
fig.update_traces(quartilemethod='linear',
scalemode='count',
meanline=dict(visible=False),
)
#iplot(fig, filename = 'figure3', config = config)
plot(fig, filename = 'figure3a.html', config = config)
# Configurations
database_path = Path('analysis/databases/3T_human_T1maps_database.pkl')
#Load database
df = pd.read_pickle(database_path)
# Prepare stats table
columns = [
'genu WM',
'splenium WM',
'cortical GM',
'deep GM'
]
col_vals = [
None,
None,
None,
None
]
df_setup = {
'all submissions mean T1': col_vals,
'inter-submission mean T1': col_vals,
'intra-submission mean T1': col_vals,
'all submissions T1 STD': col_vals,
'inter-submission T1 STD': col_vals,
'intra-submission T1 STD': col_vals,
'all submissions COV [%]': col_vals,
'inter-submission COV [%]': col_vals,
'intra-submission COV [%]': col_vals
}
stats_table = pd.DataFrame.from_dict(df_setup, orient='index', columns=columns)
## Inter-submission stats
# One subject/measurement per submission were selected. The protocol closest to the proposed one was selected, preferring complex data over magnitude-only.
# Selecting one subject/measurement per submission, protocol closest to proposed, complex if available.
ids_intersubmissions = (
1.001,
2.003,
3.001,
5.001,
6.001,
7.001,
8.002,
9.001,
10.001
)
genu_estimate = np.array([])
genu_std = np.array([])
splenium_estimate = np.array([])
splenium_std = np.array([])
deepgm_estimate = np.array([])
deepgm_std = np.array([])
cgm_estimate = np.array([])
cgm_std = np.array([])
ii = 0
for index in ids_intersubmissions:
genu_estimate = np.append(genu_estimate, np.mean(df.loc[index]['T1 - genu (WM)']))
splenium_estimate = np.append(splenium_estimate, np.mean(df.loc[index]['T1 - splenium (WM)']))
deepgm_estimate = np.append(deepgm_estimate, np.mean(df.loc[index]['T1 - deep GM']))
cgm_estimate = np.append(cgm_estimate, np.mean(df.loc[index]['T1 - cortical GM']))
ii = ii +1
stats_table['genu WM']['inter-submission mean T1'] = np.nanmean(genu_estimate)
stats_table['genu WM']['inter-submission T1 STD'] = np.nanstd(genu_estimate)
stats_table['genu WM']['inter-submission COV [%]'] = np.divide(np.nanstd(genu_estimate),np.nanmean(genu_estimate)) * 100
stats_table['splenium WM']['inter-submission mean T1'] = np.nanmean(splenium_estimate)
stats_table['splenium WM']['inter-submission T1 STD'] = np.nanstd(splenium_estimate)
stats_table['splenium WM']['inter-submission COV [%]'] = np.divide(np.nanstd(splenium_estimate),np.nanmean(splenium_estimate)) * 100
stats_table['cortical GM']['inter-submission mean T1'] = np.nanmean(cgm_estimate)
stats_table['cortical GM']['inter-submission T1 STD'] = np.nanstd(cgm_estimate)
stats_table['cortical GM']['inter-submission COV [%]'] = np.divide(np.nanstd(cgm_estimate),np.nanmean(cgm_estimate)) * 100
stats_table['deep GM']['inter-submission mean T1'] = np.nanmean(deepgm_estimate)
stats_table['deep GM']['inter-submission T1 STD'] = np.nanstd(deepgm_estimate)
stats_table['deep GM']['inter-submission COV [%]'] = np.divide(np.nanstd(deepgm_estimate),np.nanmean(deepgm_estimate)) * 100
genu_estimate_inter = genu_estimate
splenium_estimate_inter = splenium_estimate
deepgm_estimate_inter = deepgm_estimate
cgm_estimate_inter = cgm_estimate
## Intra-submission stats
#All unique T1 maps from Site 9 were used for the stats calculations. Site 9 acquired maps on 3 different scanners, 2 different vendors.
# Selecting one submission
ids_intrasubmissions = (
9.001,
9.002,
9.006,
9.007,
9.009,
9.01,
9.012,
9.013,
9.015,
9.016,
9.018,
9.019,
9.02,
9.021,
9.023,
9.025,
9.027,
9.028,
9.03,
9.031,
9.033,
9.034,
9.036,
9.037
)
genu_estimate = np.array([])
genu_std = np.array([])
splenium_estimate = np.array([])
splenium_std = np.array([])
deepgm_estimate = np.array([])
deepgm_std = np.array([])
cgm_estimate = np.array([])
cgm_std = np.array([])
ii = 0
for index in ids_intrasubmissions:
genu_estimate = np.append(genu_estimate, np.mean(df.loc[index]['T1 - genu (WM)']))
splenium_estimate = np.append(splenium_estimate, np.mean(df.loc[index]['T1 - splenium (WM)']))
deepgm_estimate = np.append(deepgm_estimate, np.mean(df.loc[index]['T1 - deep GM']))
cgm_estimate = np.append(cgm_estimate, np.mean(df.loc[index]['T1 - cortical GM']))
ii = ii +1
stats_table['genu WM']['intra-submission mean T1'] = np.nanmean(genu_estimate)
stats_table['genu WM']['intra-submission T1 STD'] = np.nanstd(genu_estimate)
stats_table['genu WM']['intra-submission COV [%]'] = np.divide(np.nanstd(genu_estimate),np.nanmean(genu_estimate)) * 100
stats_table['splenium WM']['intra-submission mean T1'] = np.nanmean(splenium_estimate)
stats_table['splenium WM']['intra-submission T1 STD'] = np.nanstd(splenium_estimate)
stats_table['splenium WM']['intra-submission COV [%]'] = np.divide(np.nanstd(splenium_estimate),np.nanmean(splenium_estimate)) * 100
stats_table['cortical GM']['intra-submission mean T1'] = np.nanmean(cgm_estimate)
stats_table['cortical GM']['intra-submission T1 STD'] = np.nanstd(cgm_estimate)
stats_table['cortical GM']['intra-submission COV [%]'] = np.divide(np.nanstd(cgm_estimate),np.nanmean(cgm_estimate)) * 100
stats_table['deep GM']['intra-submission mean T1'] = np.nanmean(deepgm_estimate)
stats_table['deep GM']['intra-submission T1 STD'] = np.nanstd(deepgm_estimate)
stats_table['deep GM']['intra-submission COV [%]'] = np.divide(np.nanstd(deepgm_estimate),np.nanmean(deepgm_estimate)) * 100
genu_estimate_intra = genu_estimate
splenium_estimate_intra = splenium_estimate
deepgm_estimate_intra = deepgm_estimate
cgm_estimate_intra = cgm_estimate
# Violin plots
import seaborn as sns
import matplotlib.pyplot as plt
# Combine data into a single DataFrame
df = pd.DataFrame({
'T1 (ms)': np.concatenate([genu_estimate_inter, genu_estimate_intra, splenium_estimate_inter, splenium_estimate_intra, cgm_estimate_inter, cgm_estimate_intra, deepgm_estimate_inter, deepgm_estimate_intra]),
'Group': ['Genu'] * len(genu_estimate_inter) + ['Genu'] * len(genu_estimate_intra) + ['Splenium'] * len(splenium_estimate_inter) + ['Splenium'] * len(splenium_estimate_intra) + ['Cgm'] * len(cgm_estimate_inter) + ['Cgm'] * len(cgm_estimate_intra) + ['DeepGM'] * len(deepgm_estimate_inter) + ['DeepGM'] * len(deepgm_estimate_intra),
'Type': ['Inter'] * len(genu_estimate_inter) + ['Intra'] * len(genu_estimate_intra) + ['Inter'] * len(splenium_estimate_inter) + ['Intra'] * len(splenium_estimate_intra) + ['Inter'] * len(cgm_estimate_inter) + ['Intra'] * len(cgm_estimate_intra) + ['Inter'] * len(deepgm_estimate_inter) + ['Intra'] * len(deepgm_estimate_intra),
'Region': ['Genu'] * len(genu_estimate_inter) + ['Genu'] * len(genu_estimate_intra) + ['Splenium'] * len(splenium_estimate_inter) + ['Splenium'] * len(splenium_estimate_intra) + ['Cgm'] * len(cgm_estimate_inter) + ['Cgm'] * len(cgm_estimate_intra) + ['DeepGM'] * len(deepgm_estimate_inter) + ['DeepGM'] * len(deepgm_estimate_intra),
})
from IPython.display import display, HTML
from plotly import __version__
from plotly.offline import init_notebook_mode, iplot, plot
config={
'showLink': False,
'displayModeBar': False,
'toImageButtonOptions': {
'format': 'png', # one of png, svg, jpeg, webp
'filename': 'custom_image',
'height': 400,
'width': 800,
'scale': 2 # Multiply title/legend/axis/canvas sizes by this factor
}
}
init_notebook_mode(connected=True)
from plotly.subplots import make_subplots
import plotly.graph_objects as go
import seaborn as sns
# Set the color palette
inter_color='rgb(113, 180, 159)'
intra_color='rgb(233, 150, 117)'
import pandas as pd
fig = go.Figure()
df1 = pd.DataFrame({
'T1 (ms)': np.concatenate([genu_estimate_inter, splenium_estimate_inter, cgm_estimate_inter, deepgm_estimate_inter]),
'Group': ['Genu'] * len(genu_estimate_inter) + ['Splenium'] * len(splenium_estimate_inter) + ['Cgm'] * len(cgm_estimate_inter) + ['DeepGM'] * len(deepgm_estimate_inter) ,
'Type': ['Inter'] * len(genu_estimate_inter) + ['Inter'] * len(splenium_estimate_inter) + ['Inter'] * len(cgm_estimate_inter) + ['Inter'] * len(deepgm_estimate_inter) ,
'Region': ['<b>Genu</b>'] * len(genu_estimate_inter) + ['<b>Splenium</b>'] * len(splenium_estimate_inter) + ['<b>cGM</b>'] * len(cgm_estimate_inter) + ['<b>Deep GM</b>'] * len(deepgm_estimate_inter) ,
})
df2 = pd.DataFrame({
'T1 (ms)': np.concatenate([genu_estimate_intra, splenium_estimate_intra, cgm_estimate_intra, deepgm_estimate_intra]),
'Group': ['Genu'] * len(genu_estimate_intra) + ['Splenium'] * len(splenium_estimate_intra) + ['Cgm'] * len(cgm_estimate_intra) + ['DeepGM'] * len(deepgm_estimate_intra) ,
'Type': ['Intra'] * len(genu_estimate_intra) + ['Intra'] * len(splenium_estimate_intra) + ['Intra'] * len(cgm_estimate_intra) + ['Intra'] * len(deepgm_estimate_intra) ,
'Region': ['<b>Genu</b>'] * len(genu_estimate_intra) + ['<b>Splenium</b>'] * len(splenium_estimate_intra) + ['<b>cGM</b>'] * len(cgm_estimate_intra) + ['<b>Deep GM</b>'] * len(deepgm_estimate_intra) ,
})
fig.add_trace(go.Violin(x=df1['Region'],
y=df1['T1 (ms)'],
side='negative',
line_color='black',
fillcolor=inter_color,
line=dict(width=1.5),
points=False,
width=1.15,
showlegend=False
)
)
fig.add_trace(go.Violin(x=df2['Region'],
y=df2['T1 (ms)'],
side='positive',
line_color='black',
fillcolor=intra_color,
line=dict(width=1.5),
points=False,
width=1.15,
showlegend=False
)
)
fig.update_layout(violingap=0, violinmode='overlay')
#fig.show()
fig.update_xaxes(
type="category",
autorange=False,
range=[-0.6,3.5],
dtick=1,
showgrid=False,
gridwidth =1,
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=22,
),
)
fig.update_yaxes(
title='<b>T<sub>1</sub> (ms)</b>',
autorange=False,
range=[600, 2500],
showgrid=True,
dtick=250,
gridcolor='rgb(169,169,169)',
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=22,
),
)
fig.update_layout(
width=800,
height=400,
margin=go.layout.Margin(
l=80,
r=40,
b=80,
t=10,
),
font=dict(
family='Times New Roman',
size=22
),
paper_bgcolor='rgb(255, 255, 255)',
plot_bgcolor='rgb(255, 255, 255)',
annotations=[
dict(
x=-0.1,
y=-0.22,
showarrow=False,
text='<b>b</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
]
)
# update characteristics shared by all traces
fig.update_traces(quartilemethod='linear',
scalemode='count',
meanline=dict(visible=False),
)
#iplot(fig, filename = 'figure3', config = config)
plot(fig, filename = 'figure3b.html', config = config)
Figure 3 Summary of results of the challenge as violin plots displaying the inter- and intra- submission dataset comparisons for phantoms (a) and human brains (b). Green indicates submissions used for inter-submission analyses, and orange indicates the sites used for intra-submission analyses.
A scatterplot of the T1 data for all submissions and their ROIs is shown in Figure 4 (phantom a-c, and human brains d-f). The NIST phantom T1 measurements are presented in each plot for different axes types (linear, log, and error) to better visualize the results. Figure 4-a shows good agreement for this dataset in comparison with the temperature-corrected reference T1 values. However, this trend did not persist for low T1 values (T1 < 100-200 ms), as seen in the log-log plot (Figure 4-b), which was expected because the imaging protocol is optimized for human brain T1 values (T1 > 500 ms). Higher variability is seen at long T1 values (T1 ~ 2000 ms) in Figure 4-a. Errors exceeding 10% are observed in the phantom spheres with T1 values below 300 ms (Figure 4-c), and 3-4 measurements with outlier values exceeding 10% error were observed in the human brain tissue range (~500-2000 ms).
Figure 4 d-f displays the scatter plot data for human datasets submitted to this challenge, showing mean and standard deviation T1 values for the WM (genu and splenium) and GM (cerebral cortex and deep GM) ROIs. Mean WM T1 values across all submissions were 828 ± 38 ms in the genu and 852 ± 49 ms in the splenium, and mean GM T1 values were 1548 ± 156 ms in the cortex and 1188 ± 133 ms in the deep GM, with less variations overall in WM compared to GM, possibly due to better ROI placement and less partial voluming in WM. The lower standard deviations for the ROIs of human database ID site 9 (by submission 18, Figure 1, and seen in orange in Figure 4d-g) are due to good slice positioning, cutting through the AC-PC line and the genu for proper ROI placement, particularly for the corpus callosum and deep GM.
# PYTHON CODE
# Module imports
# Base python
import os
from os import path
from pathlib import Path
import markdown
import random
# Graphical
import matplotlib.pyplot as plt
from PIL import Image
from matplotlib.image import imread
import matplotlib.colors
import plotly.graph_objs as go
from IPython.display import display, HTML
from plotly import __version__
from plotly.offline import init_notebook_mode, iplot, plot
config={
'showLink': False,
'displayModeBar': False,
'toImageButtonOptions': {
'format': 'png', # one of png, svg, jpeg, webp
'filename': 'custom_image',
'height': 300,
'width': 960,
'scale': 2 # Multiply title/legend/axis/canvas sizes by this factor
}
}
init_notebook_mode(connected=True)
from plotly.subplots import make_subplots
import plotly.graph_objects as go
import seaborn as sns
# Set the color palette
pal=sns.color_palette("Set2")
# Scientific
import numpy as np
from scipy.integrate import quad
import scipy.io
# Data
from repo2data.repo2data import Repo2Data
# Warnings
import warnings
warnings.filterwarnings('ignore')
if build == 'latest':
if path.isdir('analysis')== False:
!git clone https://github.com/rrsg2020/analysis.git
dir_name = 'analysis'
analysis = os.listdir(dir_name)
for item in analysis:
if item.endswith(".ipynb"):
os.remove(os.path.join(dir_name, item))
if item.endswith(".md"):
os.remove(os.path.join(dir_name, item))
elif build == 'archive':
if os.path.isdir(Path('../data')):
data_path = ['../data/rrsg-2020-note/rrsg-2020-neurolibre']
else:
# define data requirement path
data_req_path = os.path.join("..", "binder", "data_requirement.json")
# download data
repo2data = Repo2Data(data_req_path)
data_path = repo2data.install()
# Imports
import warnings
warnings.filterwarnings("ignore")
from pathlib import Path
import pandas as pd
import json
import nibabel as nib
import numpy as np
from analysis.src.database import *
from analysis.src.nist import get_reference_NIST_values, get_NIST_ids
from analysis.src.tools import calc_error
from analysis.src.nist import temperature_correction
import matplotlib.pyplot as plt
plt.style.use('analysis/custom_matplotlibrc')
plt.rcParams["figure.figsize"] = (10,10)
fig_id = 0
if build == 'latest':
database_path = Path('analysis/databases/3T_NIST_T1maps_database.pkl')
output_folder = Path("analysis/plots/03_singledataset_scatter_NIST-temperature-corrected/")
elif build=='archive':
database_path = Path(data_path[0] + '/analysis/databases/3T_NIST_T1maps_database.pkl')
output_folder = Path(data_path[0] + '/analysis/plots/03_singledataset_scatter_NIST-temperature-corrected/')
estimate_type = 'mean' # median or mean
## Define Functions
def plot_single_scatter(x, y, y_std,
title, x_label, y_label,
file_prefix, folder_path, fig_id,
y_type='linear'):
if y_type == 'linear':
plt.errorbar(x,y, y_std, fmt='o', solid_capstyle='projecting')
ax = plt.gca()
ax.axline((1, 1), slope=1, linestyle='dashed')
ax.set_ylim(ymin=0, ymax=2500)
ax.set_xlim(xmin=0, xmax=2500)
if y_type == 'log':
plt.loglog(x,y,'o')
ax = plt.gca()
ax.set_ylim(ymin=20, ymax=2500)
ax.set_xlim(xmin=20, xmax=2500)
if y_type == 'error_t1':
plt.errorbar(x,calc_error(x,y), fmt='o')
ax = plt.gca()
ax.axline((1, 0), slope=0, color='k')
ax.axline((1, -10), slope=0, linestyle='dashed', color='k')
ax.axline((1, 10), slope=0, linestyle='dashed', color='k')
ax.set_ylim(ymin=-100, ymax=100)
ax.set_xlim(xmin=0, xmax=2500)
plt.title(title)
plt.xlabel(x_label)
plt.ylabel(y_label)
fig = plt.gcf()
folder_path.mkdir(parents=True, exist_ok=True)
if fig_id<10:
filename = "0" + str(fig_id) + "_" + file_prefix
else:
filename = str(fig_id) + "_" + file_prefix
fig.savefig(folder_path / (str(filename) + '.svg'), facecolor='white')
fig.savefig(folder_path / (str(filename) + '.png'), facecolor='white')
fig_id = fig_id + 1
plt.show()
return fig_id
## Load database
df = pd.read_pickle(database_path)
## Initialize array
dataset_mean = np.zeros((1,14))
dataset_std = np.zeros((1,14))
version = np.array([])
temperature = np.array([])
ref_values = np.zeros((1,14))
intra_bool = np.array([])
ii=0
for index, row in df.iterrows():
intra_bool = np.append(intra_bool, round(index)==6)
if type(df.loc[index]['T1 - NIST sphere 1']) is np.ndarray:
version = np.append(version,df.loc[index]['phantom serial number'])
temperature = np.append(temperature, df.loc[index]['phantom temperature'])
if version[ii] == None:
version[ii] = 999 # Missing version, only known case is one where we have version > 42 right now.
if temperature[ii] == None:
temperature[ii] = 20 # Missing temperature, assume it to be 20C (reference temperature).
if ii==0:
ref_values = get_reference_NIST_values(version[ii])
temp_corrected_ref_values = temperature_correction(temperature[ii], version[ii])
else:
ref_values = np.vstack((ref_values, get_reference_NIST_values(version[ii])))
temp_corrected_ref_values = np.vstack((temp_corrected_ref_values, temperature_correction(temperature[ii], version[ii])))
tmp_dataset_estimate = np.array([])
tmp_dataset_std = np.array([])
for key in get_NIST_ids():
if estimate_type == 'mean':
tmp_dataset_estimate = np.append(tmp_dataset_estimate, np.mean(df.loc[index][key]))
elif estimate_type == 'median':
tmp_dataset_estimate = np.append(tmp_dataset_estimate, np.median(df.loc[index][key]))
else:
Exception('Unsupported dataset estimate type.')
tmp_dataset_std = np.append(tmp_dataset_std, np.std(df.loc[index][key]))
if ii==0:
dataset_estimate = tmp_dataset_estimate
dataset_std = tmp_dataset_std
else:
dataset_estimate = np.vstack((dataset_estimate, tmp_dataset_estimate))
dataset_std = np.vstack((dataset_std, tmp_dataset_std))
ii=ii+1
## Setup for plots
fig_id = 0
dims=ref_values.shape
file_prefix = 'alldatasets'
fig = make_subplots(rows=1, cols=3, horizontal_spacing = 0.08)
data_lin_intra=[]
data_lin_inter=[]
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgba(252, 141, 98, 0.5)'
marker_zorder=1
else:
marker_color='rgba(102, 194, 165, 0.5)'
marker_zorder=-1
data_lin=go.Scatter(
x=temp_corrected_ref_values[ii,:],
y=dataset_estimate[ii,:],
error_y=dict(
type='data', # value of error bar given in data coordinates
array=dataset_std[ii,:],
visible=True),
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
# For z-ordering
if bool(intra_bool[ii]):
data_lin_intra.append(data_lin)
else:
data_lin_inter.append(data_lin)
# For z-ordering
for trace in data_lin_inter:
fig.add_trace(
trace,
row=1, col=1
)
for trace in data_lin_intra:
fig.add_trace(
trace,
row=1, col=1
)
data_log_intra=[]
data_log_inter=[]
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgba(252, 141, 98, 0.5)'
marker_zorder=1
else:
marker_color='rgba(102, 194, 165, 0.5)'
marker_zorder=-1
data_log=go.Scatter(
x=temp_corrected_ref_values[ii,:],
y=dataset_estimate[ii,:],
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
# For z-ordering
if bool(intra_bool[ii]):
data_log_intra.append(data_log)
else:
data_log_inter.append(data_log)
# For z-ordering
for trace in data_log_inter:
fig.add_trace(
trace,
row=1, col=2
)
for trace in data_log_intra:
fig.add_trace(
trace,
row=1, col=2
)
data_error_intra=[]
data_error_inter=[]
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgba(252, 141, 98, 0.5)'
marker_zorder=1
else:
marker_color='rgba(102, 194, 165, 0.5)'
marker_zorder=-1
data_error=go.Scatter(
x=temp_corrected_ref_values[ii,:],
y= calc_error(temp_corrected_ref_values[ii,:],dataset_estimate[ii,:]),
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
# For z-ordering
if bool(intra_bool[ii]):
data_error_intra.append(data_error)
else:
data_error_inter.append(data_error)
# For z-ordering
for trace in data_error_inter:
fig.add_trace(
trace,
row=1, col=3
)
for trace in data_error_intra:
fig.add_trace(
trace,
row=1, col=3
)
fig.update_xaxes(
type="linear",
range=[0,2500],
title='<b>Reference T<sub>1</sub> (ms)</b>',
showgrid=True,
gridcolor='rgb(169,169,169)',
tick0 = 0,
dtick = 500,
title_font_family="Times New Roman",
title_font_size = 20,
linecolor='black',
linewidth=2,
row=1, col=1
)
fig.update_yaxes(
type="linear",
range=[0,2500],
title={
'text':'<b>T<sub>1</sub> estimate (ms)</b>',
'standoff':0
},
showgrid=True,
gridcolor='rgb(169,169,169)',
tick0 = 0,
dtick = 500,
title_font_family="Times New Roman",
title_font_size = 20,
linecolor='black',
linewidth=2,
row=1, col=1
)
fig.update_xaxes(
type="log",
range=[np.log10(20),np.log10(2500)],
title='<b>Reference T<sub>1</sub> (ms)</b>',
showgrid=True,
gridcolor='rgb(169,169,169)',
minor=dict(ticks="inside", ticklen=6, showgrid=True),
title_font_family="Times New Roman",
title_font_size = 20,
linecolor='black',
linewidth=2,
row=1, col=2
)
fig.update_yaxes(
type="log",
range=[np.log10(20),np.log10(2500)],
title={
'text':'<b>T<sub>1</sub> estimate (ms)</b>',
'standoff':0
},
showgrid=True,
gridcolor='rgb(169,169,169)',
minor=dict(ticks="inside", ticklen=6, showgrid=True),
title_font_family="Times New Roman",
title_font_size = 20,
linecolor='black',
linewidth=2,
row=1, col=2)
fig.update_xaxes(
type="linear",
range=[0,2500],
title='<b>Reference T<sub>1</sub> (ms)</b>',
showgrid=True,
gridcolor='rgb(169,169,169)',
tick0 = 0,
dtick = 500,
title_font_family="Times New Roman",
title_font_size = 20,
linecolor='black',
linewidth=2,
row=1, col=3)
fig.update_yaxes(
type="linear",
range=[-100,100],
title={
'text':'<b>Error (%)</b>',
'standoff':0
},
showgrid=True,
gridcolor='rgb(169,169,169)',
tick0 = -100,
dtick = 25,
title_font_family="Times New Roman",
title_font_size = 20,
linecolor='black',
linewidth=2,
row=1, col=3,
)
fig.update_layout(
margin=dict(l=30, r=30, t=10, b=30),
paper_bgcolor='rgb(255, 255, 255)',
plot_bgcolor='rgb(255, 255, 255)',
legend_title="",
annotations=[
dict(
x=-0.05,
y=-0.22,
showarrow=False,
text='<b>a</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=0.3,
y=-0.22,
showarrow=False,
text='<b>b</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=0.68,
y=-0.22,
showarrow=False,
text='<b>c</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=1,
y=0.99,
showarrow=False,
text='<b>Inter-sites</b>',
font=dict(
family='Times New Roman',
size=20,
),
xref='paper',
yref='paper',
bgcolor='rgba(102, 194, 165, 0.8)'
),
dict(
x=1,
y=0.871,
showarrow=False,
text='<b>Intra-sites</b>',
font=dict(
family='Times New Roman',
size=20,
),
xref='paper',
yref='paper',
bgcolor='rgba(252, 141, 98, 0.8)'
),
]
)
fig.update_layout(height=300, width=960)
#iplot(fig, filename = 'figure4a', config = config)
plot(fig, filename = 'figure4a.html', config = config)
from os import path
import os
import seaborn as sns
if build == 'latest':
if path.isdir('analysis')== False:
!git clone https://github.com/rrsg2020/analysis.git
dir_name = 'analysis'
analysis = os.listdir(dir_name)
for item in analysis:
if item.endswith(".ipynb"):
os.remove(os.path.join(dir_name, item))
if item.endswith(".md"):
os.remove(os.path.join(dir_name, item))
elif build == 'archive':
if os.path.isdir(Path('../data')):
data_path = ['../data/rrsg-2020-note/rrsg-2020-neurolibre']
else:
# define data requirement path
data_req_path = os.path.join("..", "binder", "data_requirement.json")
# download data
repo2data = Repo2Data(data_req_path)
data_path = repo2data.install()
# Imports
import warnings
warnings.filterwarnings("ignore")
from pathlib import Path
import pandas as pd
import nibabel as nib
import numpy as np
from analysis.src.database import *
import matplotlib.pyplot as plt
plt.style.use('analysis/custom_matplotlibrc')
plt.rcParams["figure.figsize"] = (20,5)
fig_id = 0
# Configurations
if build == 'latest':
database_path = Path('analysis/databases/3T_human_T1maps_database.pkl')
output_folder = Path("analysis/plots/08_wholedataset_scatter_Human/")
elif build=='archive':
database_path = Path(data_path[0] + '/analysis/databases/3T_human_T1maps_database.pkl')
output_folder = Path(data_path[0] + '/analysis/plots/08_wholedataset_scatter_Human/')
estimate_type = 'mean' # median or mean
# Load database
df = pd.read_pickle(database_path)
genu_estimate = np.array([])
genu_std = np.array([])
splenium_estimate = np.array([])
splenium_std = np.array([])
deepgm_estimate = np.array([])
deepgm_std = np.array([])
cgm_estimate = np.array([])
cgm_std = np.array([])
intra_bool = np.array([])
ii = 0
for index, row in df.iterrows():
intra_bool = np.append(intra_bool, round(index)==9)
if estimate_type == 'mean':
genu_estimate = np.append(genu_estimate, np.mean(df.loc[index]['T1 - genu (WM)']))
genu_std = np.append(genu_std, np.std(df.loc[index]['T1 - genu (WM)']))
splenium_estimate = np.append(splenium_estimate, np.mean(df.loc[index]['T1 - splenium (WM)']))
splenium_std = np.append(splenium_std, np.std(df.loc[index]['T1 - splenium (WM)']))
deepgm_estimate = np.append(deepgm_estimate, np.mean(df.loc[index]['T1 - deep GM']))
deepgm_std = np.append(deepgm_std, np.std(df.loc[index]['T1 - deep GM']))
cgm_estimate = np.append(cgm_estimate, np.mean(df.loc[index]['T1 - cortical GM']))
cgm_std = np.append(cgm_std, np.std(df.loc[index]['T1 - cortical GM']))
elif estimate_type == 'median':
genu_estimate = np.append(genu_estimate, np.median(df.loc[index]['T1 - genu (WM)']))
genu_std = np.append(genu_std, np.std(df.loc[index]['T1 - genu (WM)']))
splenium_estimate = np.append(splenium_estimate, np.median(df.loc[index]['T1 - splenium (WM)']))
splenium_std = np.append(splenium_std, np.std(df.loc[index]['T1 - splenium (WM)']))
deepgm_estimate = np.append(deepgm_estimate, np.median(df.loc[index]['T1 - deep GM']))
deepgm_std = np.append(deepgm_std, np.std(df.loc[index]['T1 - deep GM']))
cgm_estimate = np.append(cgm_estimate, np.median(df.loc[index]['T1 - cortical GM']))
cgm_std = np.append(cgm_std, np.std(df.loc[index]['T1 - cortical GM']))
else:
Exception('Unsupported dataset estimate type.')
ii = ii +1
# Store the IDs
indexes_numbers = df.index
indexes_strings = indexes_numbers.map(str)
x1_label='Site #'
x2_label='<b>Site #.Meas #</b>'
y_label="<b>T$_1$ (ms)</b>"
file_prefix = 'WM_and_GM'
folder_path=output_folder
x1=indexes_numbers
x2=indexes_strings
y=genu_estimate
y_std=genu_std
# Paper formatting of x tick labels (remove leading zero, pad zero at the end for multiples of 10)
x3=[]
for num in x2:
x3.append(num.replace('.0', '.'))
index=0
for num in x3:
if num[-3] != '.':
x3[index]=num+'0'
index+=1
# PYTHON CODE
# Module imports
import matplotlib.pyplot as plt
from PIL import Image
from matplotlib.image import imread
import scipy.io
import plotly.graph_objs as go
import numpy as np
from plotly import __version__
from plotly.offline import init_notebook_mode, iplot, plot
config={
'showLink': False,
'displayModeBar': False,
'toImageButtonOptions': {
'format': 'png', # one of png, svg, jpeg, webp
'filename': 'custom_image',
'height': 800,
'width': 960,
'scale': 2 # Multiply title/legend/axis/canvas sizes by this factor
}
}
init_notebook_mode(connected=True)
from IPython.display import display, HTML
import os
import markdown
import random
from scipy.integrate import quad
import warnings
warnings.filterwarnings('ignore')
config={
'showLink': False,
'displayModeBar': False,
'toImageButtonOptions': {
'format': 'png', # one of png, svg, jpeg, webp
'filename': 'custom_image',
'height': 800,
'width': 960,
'scale': 2 # Multiply title/legend/axis/canvas sizes by this factor
}
}
dims=genu_estimate.shape
fig = make_subplots(rows=4, cols=1, vertical_spacing = 0.07)
#data_genu=go.Scatter(
# x=x3,
# y=genu_estimate,
# error_y=dict(
# type='data', # value of error bar given in data coordinates
# array=genu_std,
# visible=True),
# mode = 'markers',
# marker=dict(color='#007ea7'),
# visible = True,
# showlegend = False
#
# )
# Genu
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgb(252, 141, 98)'
else:
marker_color='rgb(102, 194, 165)'
data=go.Scatter(
x=[x3[ii]],
y=[genu_estimate[ii]],
error_y=dict(
type='data', # value of error bar given in data coordinates
array=[genu_std[ii]],
visible=True),
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
fig.add_trace(
data,
row=1, col=1
)
# Splenium
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgb(252, 141, 98)'
else:
marker_color='rgb(102, 194, 165)'
data=go.Scatter(
x=[x3[ii]],
y=[splenium_estimate[ii]],
error_y=dict(
type='data', # value of error bar given in data coordinates
array=[splenium_std[ii]],
visible=True),
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
fig.add_trace(
data,
row=2, col=1
)
# cGM
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgb(252, 141, 98)'
else:
marker_color='rgb(102, 194, 165)'
data=go.Scatter(
x=[x3[ii]],
y=[cgm_estimate[ii]],
error_y=dict(
type='data', # value of error bar given in data coordinates
array=[cgm_std[ii]],
visible=True),
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
fig.add_trace(
data,
row=3, col=1
)
# DeepGM
for ii in range(dims[0]):
if bool(intra_bool[ii]):
marker_color='rgb(252, 141, 98)'
else:
marker_color='rgb(102, 194, 165)'
data=go.Scatter(
x=[x3[ii]],
y=[deepgm_estimate[ii]],
error_y=dict(
type='data', # value of error bar given in data coordinates
array=[deepgm_std[ii]],
visible=True),
name = 'id: '+ str(df.index[ii]),
mode = 'markers',
visible = True,
showlegend = False,
marker=dict(
color=marker_color
)
)
fig.add_trace(
data,
row=4, col=1
)
fig.update_xaxes(
autorange=False,
range=[0,57],
showgrid=False,
linecolor='black',
linewidth=2,
tickangle = -90,
tickmode='linear',
tickfont=dict(
family='Times New Roman',
size=12,
),
title_font_family="Times New Roman",
row=1, col=1
)
fig.update_yaxes(
title='<b>T<sub>1</sub> (ms)</b>',
autorange=True,
showgrid=True,
dtick=100,
gridcolor='rgb(169,169,169)',
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=18,
),
title_font_family="Times New Roman",
row=1, col=1
)
fig.update_xaxes(
autorange=False,
range=[0,57],
showgrid=False,
linecolor='black',
linewidth=2,
tickangle = -90,
tickmode='linear',
tickfont=dict(
family='Times New Roman',
size=12,
),
title_font_family="Times New Roman",
row=2, col=1
)
fig.update_yaxes(
title='<b>T<sub>1</sub> (ms)</b>',
autorange=True,
showgrid=True,
dtick=100,
gridcolor='rgb(169,169,169)',
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=18,
),
title_font_family="Times New Roman",
row=2, col=1
)
fig.update_xaxes(
autorange=False,
range=[0,57],
showgrid=False,
linecolor='black',
linewidth=2,
tickangle = -90,
tickmode='linear',
tickfont=dict(
family='Times New Roman',
size=12,
),
title_font_family="Times New Roman",
row=3, col=1
)
fig.update_yaxes(
title='<b>T<sub>1</sub> (ms)</b>',
autorange=True,
showgrid=True,
dtick=250,
gridcolor='rgb(169,169,169)',
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=18,
),
title_font_family="Times New Roman",
row=3, col=1
)
fig.update_xaxes(
title='<b>Site #.Meas #</b>',
autorange=False,
range=[0,57],
showgrid=False,
linecolor='black',
linewidth=2,
tickangle = -90,
tickmode='linear',
tickfont=dict(
family='Times New Roman',
size=12,
),
title_font_family="Times New Roman",
row=4, col=1
)
fig.update_yaxes(
title='<b>T<sub>1</sub> (ms)</b>',
autorange=True,
showgrid=True,
dtick=250,
gridcolor='rgb(169,169,169)',
linecolor='black',
linewidth=2,
tickfont=dict(
family='Times New Roman',
size=18,
),
title_font_family="Times New Roman",
row=4, col=1
)
fig.update_layout(
width=960,
height=800,
margin=go.layout.Margin(
l=80,
r=40,
b=80,
t=10,
),
font=dict(
family='Times New Roman',
size=22
),
annotations=[
dict(
x=-0.1,
y=0.85,
showarrow=False,
text='<b>d</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=-0.1,
y=0.55,
showarrow=False,
text='<b>e</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=-0.1,
y=0.2,
showarrow=False,
text='<b>f</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=-0.1,
y=-0.1,
showarrow=False,
text='<b>g</b>',
font=dict(
family='Times New Roman',
size=64
),
xref='paper',
yref='paper'
),
dict(
x=1,
y=0.986,
showarrow=False,
text='<b>WM - Genu</b>',
font=dict(
family='Times New Roman',
size=20
),
xref='paper',
yref='paper'
),
dict(
x=1,
y=0.726,
showarrow=False,
text='<b>WM - Splenium</b>',
font=dict(
family='Times New Roman',
size=20
),
xref='paper',
yref='paper'
),
dict(
x=1,
y=0.425,
showarrow=False,
text='<b>cGM</b>',
font=dict(
family='Times New Roman',
size=20
),
xref='paper',
yref='paper'
),
dict(
x=1,
y=0.143,
showarrow=False,
text='<b>Deep GM</b>',
font=dict(
family='Times New Roman',
size=20
),
xref='paper',
yref='paper'
),
],
paper_bgcolor='rgb(255, 255, 255)',
plot_bgcolor='rgb(255, 255, 255)',
)
#iplot(fig, filename = 'figure6b', config = config)
plot(fig, filename = 'figure4d.html', config = config)
Figure 4 Measured mean T1 values vs. temperature-corrected NIST reference values of the phantom spheres are presented as linear plots (a), log-log plots (b), and plots of the error relative to the reference T1 value (c). Green indicates submissions used for inter-submission analyses, and orange indicates the sites used for intra-submission analyses. The dashed lines in plots (c) represent a ±10 % error. Mean T1 values in two sets of ROIs, white matter (one 5⨯5 voxel ROI for genu, one 5x5 voxel ROI for splenium) and gray matter (three 3⨯3 voxel ROIs for cortex, one 5x5 voxel ROI for deep GM). In subplot g), the missing datapoints for deep GM for sites 1, 8, and 10 were due to the slice positioning of the acquisition not containing deep GM.
4 | DISCUSSION#
This challenge focused on exploring if different research groups could reproduce T1 maps based on the protocol information reported in a seminal publication [Barral et al., 2010]. Eighteen submissions independently implemented the inversion recovery T1 mapping acquisition protocol as outlined in Barral et al. [Barral et al., 2010], and reported T1 mapping data in a standard quantitative MRI phantom and/or human brains at 27 MRI sites, using systems from three different vendors (GE, Philips, Siemens). The collaborative effort produced an open-source database of 94 T1 mapping datasets, including 38 ISMRM/NIST phantom and 56 human brain datasets. The inter-submission variability was twice as high as the intra-submission variability in both phantom and human brain T1 measurements, demonstrating that written instructions communicated via a PDF are not enough for reproducibility in quantitative MRI. This study reports the inherent uncertainty in T1 measures across independent research groups, which brings us one step closer to producing a practical baseline of variations for this metric.
Overall, our approach did show improvement in the reproducibility of T1 measurements in vivo compared to researchers implementing T1 mapping protocols completely independently (i.e. with no central guidance), as literature T1 values in vivo vary more than reported here (e.g., Bojorquez et al. [Bojorquez et al., 2017] reports that reported T1 values in WM vary between 699 to 1735 ms in published literature). We were aware that coordination was essential for a quantitative MRI challenge, which is why the protocol specifications we provided to researchers were more detailed than any guidelines for quantitative MR imaging that were available at the time. Yet, even in combination with the same T1 mapping processing tools, this level of description (a PDF + post-processing tools) leaves something to be desired.
This analysis highlights that more information is needed to unify all the aspects of a pulse sequence across sites, beyond what is routinely reported in a scientific publication. However, in a vendor-specific setting, this is a major challenge given the disparities between proprietary development libraries [Gracien et al., 2020]. Vendor-neutral pulse sequence design platforms [Cordes et al., 2020, Karakuzu et al., 2022, Layton et al., 2017] have emerged as a powerful solution to standardize sequence components at the implementation level (e.g., EF pulse shape, gradients, etc.). Vendor neutrality has been shown to significantly reduce the variability of T1 maps acquired using VFA across vendors [Karakuzu et al., 2022]. In the absence of a vendor-neutral framework, a vendor-specific alternative is the implementation of a strategy to control the saturation of MT across TRs [A G Teixeira et al., 2020]. Nevertheless, this approach can still benefit from a vendor-neutral protocol to enhance accessibility and unify implementations. This is because vendor-specific constraints are recognized to impose limitations on the adaptability of sequences, resulting in significant variability even when implementations are closely aligned within their respective vendor-specific development environments [Lee et al., 2019].
The 2020 Reproducibility Challenge, jointly organized by the Reproducible Research and Quantitative MR ISMRM study groups, led to the creation of a large open database of standard quantitative MR phantom and human brain inversion recovery T1 maps. These maps were measured using independently implemented imaging protocols on MRI scanners from three different manufacturers. All collected data, processing pipeline code, computational environment files, and analysis scripts were shared with the goal of promoting reproducible research practices, and an interactive dashboard was developed to broaden the accessibility and engagement of the resulting datasets (https://rrsg2020.dashboards.neurolibre.org). The differences in stability between independently implemented (inter-submission) and centrally shared (intra-submission) protocols observed both in phantoms and in vivo could help inform future meta-analyses of quantitative MRI metrics [Lazari and Lipp, 2021, Mancini et al., 2020] and better guide multi-center collaborations.
By providing access and analysis tools for this multi-center T1 mapping dataset, we aim to provide a benchmark for future T1 mapping approaches. We also hope that this dataset will inspire new acquisition, analysis, and standardization techniques that address non-physiological sources of variability in T1 mapping. This could lead to more robust and reproducible quantitative MRI and ultimately better patient care.
ACKNOWLEDGEMENT#
The conception of this collaborative reproducibility challenge originated from discussions with experts, including Paul Tofts, Joëlle Barral, and Ilana Leppert, who provided valuable insights. Additionally, Kathryn Keenan, Zydrunas Gimbutas, and Andrew Dienstfrey from NIST provided their code to generate the ROI template for the ISMRM/NIST phantom. Dylan Roskams-Edris and Gabriel Pelletier from the Tanenbaum Open Science Institute (TOSI) offered valuable insights and guidance related to data ethics and data sharing in the context of this international multi-center conference challenge. The 2020 RRSG study group committee members who launched the challenge, Martin Uecker, Florian Knoll, Nikola Stikov, Maria Eugenia Caligiuri, and Daniel Gallichan, as well as the 2020 qMRSG committee members, Kathryn Keenan, Diego Hernando, Xavier Golay, Annie Yuxin Zhang, and Jeff Gunter, also played an essential role in making this challenge possible. We would also like to thank the Canadian Open Neuroscience Platform (CONP), the Quebec Bioimaging Network (QBIN), and the Montreal Heart Institute Foundation for their support in creating the NeuroLibre preprint. Finally, we extend our thanks to all the volunteers and individuals who helped with the scanning at each imaging site.
The authors thank the ISMRM Reproducible Research Study Group for conducting a code review of the code (Version 1) supplied in the Data Availability Statement. The scope of the code review covered only the code’s ease of download, quality of documentation, and ability to run, but did not consider scientific accuracy or code efficiency.
Lastly, we acknowledge use of ChatGPT (v3), a generative language model, for accelerating manuscript preparation. The co-first authors employed ChatGPT in the initial draft for transforming bullet point sentences into paragraphs, proofreading for typos, and refining the academic tone. ChatGPT served exclusively as a writing aid, and was not used to create or interpret results.
DATA AVAILABILITY STATEMENT#
An interactive NeuroLibre preprint of this manuscript is available at https://preprint.neurolibre.org/10.55458/neurolibre.00014/. All imaging data submitted to the challenge, dataset details, registered ROI maps, and processed T1 maps are hosted on OSF https://osf.io/ywc9g/. The dataset submissions and quality assurance were handled through GitHub issues in this repository https://github.com/rrsg2020/data_submission (commit: 9d7eff1). Note that accepted submissions are closed issues, and that the GitHub branches associated with the issue numbers contain the Dockerfile and Jupyter Notebook scripts that reproduce these preliminary quality assurance results and can be run in a browser using MyBinder. The ROI registration scripts for the phantoms and the T1 fitting pipeline to process all datasets are hosted in this GitHub repository, https://github.com/rrsg2020/t1_fitting_pipeline (commit: 3497a4e). All the analyses of the datasets were done using Jupyter Notebooks and are available in this repository, https://github.com/rrsg2020/analysis (commit: 8d38644), which also contains a Dockerfile to reproduce the environment using a tool like MyBinder. A dashboard was developed to explore the datasets information and results in a browser, which is accessible here, https://rrsg2020.dashboards.neurolibre.org, and the code is also available on GitHub: https://github.com/rrsg2020/rrsg2020-dashboard (commit: 6ee9321).
References#
- 1
Rui Pedro A G Teixeira, Radhouene Neji, Tobias C Wood, Ana A Baburamani, Shaihan J Malik, and Joseph V Hajnal. Controlled saturation magnetization transfer for reproducible multivendor variable flip angle T1 and T2 mapping. Magn. Reson. Med., 84(1):221–236, July 2020. doi:10.1002/mrm.28109.
- 2
Brian B Avants, Nick Tustison, and Gang Song. Advanced normalization tools (ANTS). Insight J., 2(365):1–35, 2009. doi:10.54294/uvnhin.
- 3
Octavia Bane, Stefanie J Hectors, Mathilde Wagner, Lori L Arlinghaus, Madhava P Aryal, Yue Cao, Thomas L Chenevert, Fiona Fennessy, Wei Huang, Nola M Hylton, Jayashree Kalpathy-Cramer, Kathryn E Keenan, Dariya I Malyarenko, Robert V Mulkern, David C Newitt, Stephen E Russek, Karl F Stupic, Alina Tudorica, Lisa J Wilmes, Thomas E Yankeelov, Yi-Fei Yen, Michael A Boss, and Bachir Taouli. Accuracy, repeatability, and interplatform reproducibility of T1 quantification methods used for DCE-MRI: results from a multicenter phantom study. Magn. Reson. Med., 79(5):2564–2575, May 2018. doi:10.1002/mrm.26903.
- 4(1,2,3,4,5,6)
Joëlle K Barral, Erik Gudmundson, Nikola Stikov, Maryam Etezadi-Amoli, Petre Stoica, and Dwight G Nishimura. A robust methodology for in vivo T1 mapping. Magn. Reson. Med., 64(4):1057–1067, October 2010. doi:10.1002/mrm.22497.
- 5
Carl Boettiger. An introduction to docker for reproducible research. Oper. Syst. Rev., 49(1):71–79, January 2015. doi:10.1145/2723872.2723882.
- 6
Jorge Zavala Bojorquez, Stéphanie Bricq, Clement Acquitter, François Brunotte, Paul M Walker, and Alain Lalande. What are normal relaxation times of tissues at 3 t? Magn. Reson. Imaging, 35:69–80, January 2017. doi:10.1016/j.mri.2016.08.021.
- 7
P A Bottomley, T H Foster, R E Argersinger, and L M Pfeifer. A review of normal tissue hydrogen NMR relaxation times and relaxation mechanisms from 1-100 MHz: dependence on tissue type, NMR frequency, temperature, species, excision, and age. Med. Phys., 11(4):425–448, 1984. doi:10.1118/1.595535.
- 8
Mathieu Boudreau, Kathryn E Keenan, and Nikola Stikov. Quantitative T1 and t1r mapping. In Quantitative Magnetic Resonance Imaging, pages 19–45. November 2020. doi:10.1016/b978-0-12-817057-1.00004-4.
- 9(1,2)
Jean-François Cabana, Ye Gu, Mathieu Boudreau, Ives R Levesque, Yaaseen Atchia, John G Sled, Sridar Narayanan, Douglas L Arnold, G Bruce Pike, Julien Cohen-Adad, Tanguy Duval, Manh-Tung Vuong, and Nikola Stikov. Quantitative magnetization transfer imaging\textit madeeasy with \textit qMTLab: software for data simulation, analysis, and visualization. Concepts Magn. Reson. Part A Bridg. Educ. Res., 44A(5):263–277, September 2015. doi:10.1002/cmr.a.21357.
- 10
Hai-Ling Margaret Cheng and Graham A Wright. Rapid high-resolutiont1 mapping by variable flip angles: accurate and precise measurements in the presence of radiofrequency field inhomogeneity. 2006. doi:10.1002/mrm.20791.
- 11
Cristoffer Cordes, Simon Konstandin, David Porter, and Matthias Günther. Portable and platform-independent MR pulse sequence programs. Magn. Reson. Med., 83(4):1277–1290, April 2020. doi:10.1002/mrm.28020.
- 12
R Damadian. Tumor detection by nuclear magnetic resonance. Science, 171(3976):1151–1153, March 1971. doi:10.1126/science.171.3976.1151.
- 13
Sean C L Deoni, Brian K Rutt, and Terry M Peters. Rapid combinedt1 andt2 mapping using gradient recalled acquisition in the steady state. 2003. doi:10.1002/mrm.10407.
- 14
Matthias A Dieringer, Michael Deimling, Davide Santoro, Jens Wuerfel, Vince I Madai, Jan Sobesky, Florian von Knobelsdorff-Brenkenhoff, Jeanette Schulz-Menger, and Thoralf Niendorf. Rapid parametric mapping of the longitudinal relaxation time T1 using two-dimensional variable flip angle magnetic resonance imaging at 1.5 tesla, 3 tesla, and 7 tesla. PLoS One, 9(3):e91318, March 2014. doi:10.1371/journal.pone.0091318.
- 15
L E Drain. A direct method of measuring nuclear Spin-Lattice relaxation times. Proc. Phys. Soc. A, 62(5):301, May 1949. doi:10.1088/0370-1298/62/5/306.
- 16
R R Ernst and W A Anderson. Application of fourier transform spectroscopy to magnetic resonance. Rev. Sci. Instrum., 37(1):93–102, January 1966. doi:10.1063/1.1719961.
- 17
E K Fram, R J Herfkens, G A Johnson, G H Glover, J P Karis, A Shimakawa, T G Perkins, and N J Pelc. Rapid calculation of T1 using variable flip angle gradient refocused imaging. Magn. Reson. Imaging, 5(3):201–208, 1987. doi:10.1016/0730-725X(87)90021-X.
- 18
D G Fryback and J R Thornbury. The efficacy of diagnostic imaging. Med. Decis. Making, 11(2):88–94, 1991. doi:10.1177/0272989X9101100203.
- 19
Erwin L Hahn. An accurate nuclear magnetic resonance method for measuring Spin-Lattice relaxation times. 1949. doi:10.1103/PhysRev.76.145.
- 20(1,2)
Agah Karakuzu, Labonny Biswas, Julien Cohen-Adad, and Nikola Stikov. Vendor-neutral sequences and fully transparent workflows improve inter-vendor reproducibility of quantitative MRI. Magn. Reson. Med., 88(3):1212–1228, September 2022. doi:10.1002/mrm.29292.
- 21(1,2)
Agah Karakuzu, Mathieu Boudreau, Tanguy Duval, Tommy Boshkovski, Ilana Leppert, Jean-François Cabana, Ian Gagnon, Pascale Beliveau, G Pike, Julien Cohen-Adad, and Nikola Stikov. qMRLab: quantitative MRI analysis, under one umbrella. J. Open Source Softw., 5(53):2343, September 2020. doi:10.21105/joss.02343.
- 22
Kathryn E Keenan, Maureen Ainslie, Alex J Barker, Michael A Boss, Kim M Cecil, Cecil Charles, Thomas L Chenevert, Larry Clarke, Jeffrey L Evelhoch, Paul Finn, Daniel Gembris, Jeffrey L Gunter, Derek L G Hill, Clifford R Jack, Jr, Edward F Jackson, Guoying Liu, Stephen E Russek, Samir D Sharma, Michael Steckner, Karl F Stupic, Joshua D Trzasko, Chun Yuan, and Jie Zheng. Quantitative magnetic resonance imaging phantoms: a review and the need for a system phantom. Magn. Reson. Med., 79(1):48–61, January 2018. doi:10.1002/mrm.26982.
- 23
Kathryn E Keenan, Joshua R Biller, Jana G Delfino, Michael A Boss, Mark D Does, Jeffrey L Evelhoch, Mark A Griswold, Jeffrey L Gunter, R Scott Hinks, Stuart W Hoffman, Geena Kim, Riccardo Lattanzi, Xiaojuan Li, Luca Marinelli, Gregory J Metzger, Pratik Mukherjee, Robert J Nordstrom, Adele P Peskin, Elena Perez, Stephen E Russek, Berkman Sahiner, Natalie Serkova, Amita Shukla-Dave, Michael Steckner, Karl F Stupic, Lisa J Wilmes, Holden H Wu, Huiming Zhang, Edward F Jackson, and Daniel C Sullivan. Recommendations towards standards for quantitative MRI (qMRI) and outstanding needs. J. Magn. Reson. Imaging, 49(7):e26–e39, June 2019. doi:10.1002/jmri.26598.
- 24
Kathryn E Keenan, Zydrunas Gimbutas, Andrew Dienstfrey, Karl F Stupic, Michael A Boss, Stephen E Russek, Thomas L Chenevert, P V Prasad, Junyu Guo, Wilburn E Reddick, Kim M Cecil, Amita Shukla-Dave, David Aramburu Nunez, Amaresh Shridhar Konar, Michael Z Liu, Sachin R Jambawalikar, Lawrence H Schwartz, Jie Zheng, Peng Hu, and Edward F Jackson. Multi-site, multi-platform comparison of MRI T1 measurement using the system phantom. PLoS One, 16(6):e0252966, June 2021. doi:10.1371/journal.pone.0252966.
- 25
Thomas Kluyver, Benjamin Ragan-Kelley, Brian Granger, Matthias Bussonnier, Jonathan Frederic, Kyle Kelley, Jessica Hamrick, Jason Grout, Sylvain Corlay, Paul Ivanov, Safia Abdalla, and Carol Willing. Jupyter notebooks – a publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas, pages 87–90. IOS Press, Amsterdam, NY, 2016. doi:10.3233/978-1-61499-649-1-87.
- 26
Kelvin J Layton, Stefan Kroboth, Feng Jia, Sebastian Littin, Huijun Yu, Jochen Leupold, Jon-Fredrik Nielsen, Tony Stöcker, and Maxim Zaitsev. Pulseq: a rapid and hardware-independent pulse sequence prototyping framework. Magn. Reson. Med., 77(4):1544–1552, April 2017. doi:10.1002/mrm.26235.
- 27
Alberto Lazari and Ilona Lipp. Can MRI measure myelin? systematic review, qualitative assessment, and meta-analysis of studies validating microstructural imaging with myelin histology. Neuroimage, 230:117744, April 2021. doi:10.1016/j.neuroimage.2021.117744.
- 28
Yoojin Lee, Martina F Callaghan, Julio Acosta-Cabronero, Antoine Lutti, and Zoltan Nagy. Establishing intra- and inter-vendor reproducibility of T1 relaxation time measurements with 3T MRI. Magn. Reson. Med., 81(1):454–465, January 2019.
- 29
D C Look and D R Locker. Time saving in measurement of NMR and EPR relaxation times. Rev. Sci. Instrum., 41(2):250–251, February 1970. doi:10.1063/1.1684482.
- 30
Matteo Mancini, Agah Karakuzu, Julien Cohen-Adad, Mara Cercignani, Thomas E Nichols, and Nikola Stikov. An interactive meta-analysis of MRI biomarkers of myelin. Elife, October 2020. doi:10.55458/neurolibre.00004.
- 31
José P Marques and Rolf Gruetter. New developments and applications of the MP2RAGE sequence–focusing the contrast and high spatial resolution R1 mapping. PLoS One, 8(7):e69294, July 2013. doi:10.1371/journal.pone.0069294.
- 32
José P Marques, Tobias Kober, Gunnar Krueger, Wietske van der Zwaag, Pierre-François Van de Moortele, and Rolf Gruetter. MP2RAGE, a self bias-field corrected sequence for improved segmentation and t1-mapping at high field. 2010. doi:10.1016/j.neuroimage.2009.10.002.
- 33
Paul McCarthy. FSLeyes. September 2019. doi:10.5281/zenodo.6511596.
- 34
Dirk Merkel. Docker: lightweight linux containers for consistent development and deployment. https://www.seltzer.com/margo/teaching/CS508.19/papers/merkel14.pdf, 2014. Accessed: 2023-2-14.
- 35
Daniel R Messroghli, Aleksandra Radjenovic, Sebastian Kozerke, David M Higgins, Mohan U Sivananthan, and John P Ridgway. Modified Look-Locker inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magn. Reson. Med., 52(1):141–146, July 2004. doi:10.1002/mrm.20110.
- 36
Stefan K Piechnik, Vanessa M Ferreira, Erica Dall'Armellina, Lowri E Cochlin, Andreas Greiser, Stefan Neubauer, and Matthew D Robson. Shortened modified Look-Locker inversion recovery (ShMOLLI) for clinical myocardial t1-mapping at 1.5 and 3 T within a 9 heartbeat breathhold. J. Cardiovasc. Magn. Reson., 12(1):69, November 2010. doi:10.1186/1532-429X-12-69.
- 37
I L Pykett and P Mansfield. A line scan image study of a tumorous rat leg by NMR. Phys. Med. Biol., 23(5):961–967, September 1978. doi:10.1097/00004728-197904000-00056.
- 38
T W Redpath and F W Smith. Technical note: use of a double inversion recovery pulse sequence to image selectively grey or white brain matter. Br. J. Radiol., 67(804):1258–1263, December 1994. doi:10.1259/0007-1285-67-804-1258.
- 39
Mark Schweitzer. Stages of technical efficacy: journal of magnetic resonance imaging style. J. Magn. Reson. Imaging, 44(4):781–782, October 2016. doi:10.1002/jmri.25417.
- 40
Nicole Seiberlich, Vikas Gulani, Adrienne Campbell, Steven Sourbron, Mariya Ivanova Doneva, Fernando Calamante, and Houchun Harry Hu. Quantitative Magnetic Resonance Imaging. Academic Press, November 2020.
- 41
J G Sled and G B Pike. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn. Reson. Med., 46(5):923–931, November 2001. doi:10.1002/mrm.1278.
- 42(1,2,3)
Nikola Stikov, Mathieu Boudreau, Ives R Levesque, Christine L Tardif, Joëlle K Barral, and G Bruce Pike. On the accuracy of T1 mapping: searching for common ground. Magn. Reson. Med., 73(2):514–522, 2015. doi:10.1002/mrm.25135.
- 43(1,2)
Karl F Stupic, Maureen Ainslie, Michael A Boss, Cecil Charles, Andrew M Dienstfrey, Jeffrey L Evelhoch, Paul Finn, Zydrunas Gimbutas, Jeffrey L Gunter, Derek L G Hill, Clifford R Jack, Edward F Jackson, Todor Karaulanov, Kathryn E Keenan, Guoying Liu, Michele N Martin, Pottumarthi V Prasad, Nikki S Rentz, Chun Yuan, and Stephen E Russek. A standard system phantom for magnetic resonance imaging. Magn. Reson. Med., 86(3):1194–1211, September 2021. doi:10.1002/mrm.28779.
- 44
P S Tofts. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J. Magn. Reson. Imaging, 7(1):91–101, 1997. doi:10.1002/jmri.1880070113.
- 45
J P Wansapura, S K Holland, R S Dunn, and W S Ball, Jr. NMR relaxation times in the human brain at 3.0 tesla. J. Magn. Reson. Imaging, 9(4):531–538, April 1999. doi:10.1002/(SICI)1522-2586(199904)9:4<531::AID-JMRI4>3.0.CO;2-L.
- 46
Jing Yuan, Steven Kwok Keung Chow, David Ka Wai Yeung, Anil T Ahuja, and Ann D King. Quantitative evaluation of dual-flip-angle T1 mapping on DCE-MRI kinetic parameter estimation in head and neck. Quant. Imaging Med. Surg., 2(4):245–253, December 2012. doi:10.3978/j.issn.2223-4292.2012.11.04.
- 47
Beg, Taka, Kluyver, Konovalov, Ragan-Kelley, Thiery, and Fangohr. Using jupyter for reproducible scientific workflows. https://www.computer.org › csdl › magazine › 2021/02https://www.computer.org › csdl › magazine › 2021/02, 23:36–46, March 2021. doi:10.1109/MCSE.2021.3052101.
- 48
Gracien, Maiworm, Brüche, Shrestha, and others. How stable is quantitative MRI?–Assessment of intra-and inter-scanner-model reproducibility using identical acquisition sequences and data analysis …. Neuroimage, 2020. doi:10.1016/j.neuroimage.2019.116364.
- 49
Project Jupyter, Matthias Bussonnier, Jessica Forde, Jeremy Freeman, Brian Granger, Tim Head, Chris Holdgraf, Kyle Kelley, Gladys Nalvarte, Andrew Osheroff, M Pacer, Yuvi Panda, Fernando Perez, Benjamin Ragan-Kelley, and Carol Willing. Binder 2.0 - reproducible, interactive, sharable environments for science at scale. In Proceedings of the Python in Science Conference. SciPy, 2018. doi:10.25080/Majora-4af1f417-011.
- 1
- 2
The website provided to the researchers has since been removed from the NIST website.
- 3
- 4
This website was provided as a resource to the participants for best practices to obtain informed consent for data sharing.
- 5
Submissions were reviewed by MB and AK. Submission guidelines (https://github.com/rrsg2020/data_submission/blob/master/README.md) and a GitHub issue checklist (https://github.com/rrsg2020/data_submission/blob/master/.github/ISSUE_TEMPLATE/data-submission-request.md) were checked. Lastly, the submitted data was passed to the T1 processing pipeline and verified for quality and expected values. Feedback was sent to the authors if their submission did not adhere to the requested guidelines, or if issues with the submitted datasets were found and if possible, corrected (e.g., scaling issues between inversion time data points).
- 6
Strictly speaking, not all manufacturers operate at 3.0 T. Even though this is the field strength advertised by the system manufacturers, there is some deviation in actual field strength between vendors. The actual center frequencies are typically reported in the DICOM files, and these were shared for most datasets and are available in our OSF.io repository (https://osf.io/ywc9g/). From these datasets, the center frequencies imply participants that used GE and Philips scanners were at 3.0T (
~127.7 MHz), whereas participants that used Siemens scanners were at 2.89T (~123.2 MHz). For simplicity, we will always refer to the field strength in this article as 3T.- 7
- 8
https://github.com/qMRLab/qMRLab/blob/master/src/Models_Functions/IRfun/rdNlsPr.m#L118-L129
- 9
- 10
https://mybinder.org/v2/gh/rrsg2020/analysis/master?filepath=analysis
- 11
The T1 values vs temperature tables reported by the phantom manufacturer did not always exhibit a linear relationship. We explored the use of spline fitting on the original data and quadratic fitting on the log-log representation of the data, Both methods yielded good results, and we opted to use the latter in our analyses. The code is found here, and a Jupyter Notebook used in temperature interpolation development is here.
- 12
Only T1 maps measured using phantom version 1 were included in this inter-submission COV, as including both sets would have increased the COV due to the differences in reference T1 values. There were seven research groups that used version 1, and six that used version 2.